InGAN捕捉图像内部块
图像翻译这个领域的应用是相当的多,图像风格迁移、图像修复、图像属性变换、图像分割、图像模态的转换等都可以统称为图像翻译的任务。本文将介绍一个图像翻译中比较新颖和有趣的应用,图像的重定向,也就是对图像进行自然的放大和缩小而不影响图像的整体,这是区别于简单的图像拉伸和压缩的过程,而是通过图像到图像转换的过程来实现的。本文将介绍的InGAN通过捕获图像的内部色块分布实现了图像的的扩充和拉伸,同时文章也是ICCV 2019的oral。
论文引入
每个自然图像都有其独特的内部统计数据:构成图像的小块,这些小块在图像中多次出现,从而也可以作为该图像的特异性的表示[1]。例如,假设根据一个输入图像,希望将其转换为形状,大小和纵横比完全不同的新图像。但是又要求不能扭曲其内部任何元素,将它们全部保留为其原始大小,形状,长宽比以及图像中相同的相对位置。这个过程可以由图1所示:

图1.图像在保留内部元素下的拉伸
当放大图1中的水果摊图像时,每个水果盒中会添加更多的水果,同时保持每个水果的大小相同。反之亦然,当图像变小时,水果的数量变小,同时保持其大小和在图像中的相对位置。此外,请注意,目标图像不一定是矩形的。如果能够捕获并可视化了这种独特的图像特定小块分布,就可以将其映射到不同大小和形状的新目标图像(所有目标图像都具有与输入图像相同的内部小块分布) 。
如何才能做到这一点?满足这些标准首先是要求目标图像中的小块分布与输入图像中多个图像尺度上的小块分布相匹配,分布匹配允许合成不同大小和形状的新目标图像。双向相似性[2]是目前实现该转换最先进的方法,双向相似性变换将目标图像限制为仅包含来自输入图像的色块(“视觉一致性”),输入目标应仅包含来自目标的色块(“视觉完整性”)。因此,在目标图像中不会引入新的伪像,并且也不会丢失任何关键信息。InGAN的设计目的在双向相似性的基础上进一步实现:
- 不仅要求所有输入色块都在输出中,而且还需要保持这些色块的频率相同。
- 通过匹配分布而不是单个补丁。
- 通过已训练的网络进行一次前向遍历可以生成任何大小/形状/长宽比的目标图像。
这里实现分布的匹配就依赖于生成对抗网络(GAN)来实现了,但是InGAN并不是简单的匹配完整图像的分布,而是通过对图像的不同尺度下的分块分布进行匹配,这也正是文章的题目”InGAN: Capturing and Remapping the “DNA” of a Natural Image”的核心,实现这种内部分块分布的学习,可以进一步的理解和应用在超分辨率图像、修复从图像中删除的补丁、从图像中合成纹理等,总结一下InGAN的优势:
- InGAN为各种不同的任务和不同的数据类型提供统一的框架,所有这些都具有一个单一的网络体系结构。
- InGAN可以产生大小,形状和纵横比明显不同的输出,包括非矩形输出图像。
- InGAN是第一个在单个自然图像上训练GAN(训练过程中只是对一张图像进行训练和学习)。
InGAN框架
InGAN是如何训练一张图像达到图像重定向的呢?我们先从整体架构上去理解,图2展示了InGAN的框架:
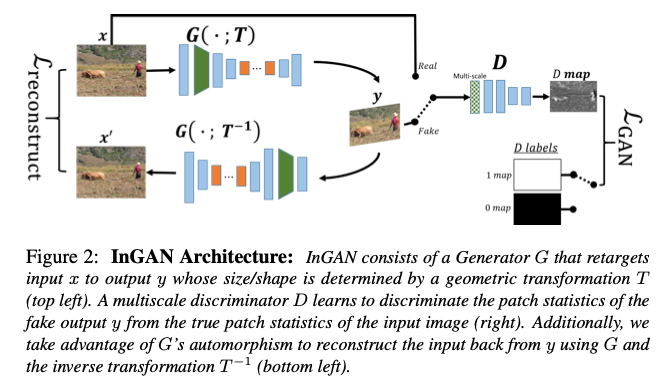
图2.InGAN整体框架
我们先宏观的分析一下InGAN模型,整体结构就是简单的由生成器和判别器构成,生成器的输入就是输入图像$x$和目标尺度$T$,得到的输出就是目标尺寸下的图像$y$。为了缓解GAN生成多样性不足的问题,这里引入了类似于”循环一致”的思想,就是将由$x$得到的$y$再次送入到生成器还原为原尺度图像$x’$,理想情况下$x$与$x’$应该完全一致。但是这个过程和CycleGAN[3]等”循环一致”是有本质区别的,CycleGAN中的生成器和判别器是有两路的,也就是由$A \to B$和$B \to A$两路,然而InGAN中是只有一路的,因为InGAN的目的是为了学习到图像的内部块,并不是对图像做任何结构和风格的变换。所以,只是图像的尺度发生了改变,这里用一个生成器就可以实现,作者也将这种设计称之为Encoder-Encoder结构。在优化阶段,判别器D是一个多尺度的判别器,它会根据对比不同尺度下的真实图像和生成图像的真假,在不同尺度下进行加权得到最后的得分,用于优化对抗损失。
整体架构分析下来可以对整个网络有了一个大概上的了解,这里涉及到的损失函数也很简单,一个是生成对抗损失,另一个就是循环一致损失:
\[\mathcal L_{GAN}(G,D) = \mathbb E_{x \sim p_{data}(x)}[(D(x)-1)^2]+\mathbb E_{x \sim p_{data}(x)} [D(G(x))^2]\]这里采用的生成对抗损失来自于LSGAN[4],循环一致损失就是重构损失:
\[\mathcal L_{reconst} = \Vert G(G(x;T);T^{-1})-1 \Vert_1\]总的损失可表示为:
\[\mathcal L_{InGAN} = \mathcal L_{GAN} + \lambda \cdot \mathcal L_{reconst}\]设计细节
如果你只是想了解一下InGAN的工作原理的话,上面一节已经大致上解释了,这一部分将对网络的具体设计细节进行讨论。
灵活的生成器
生成器的具体设计如图3所示:
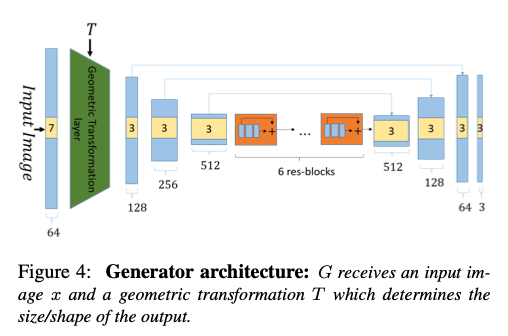
图3.InGAN中生成器的详细结构
整个生成器由三部分组成,用于上下采样和图像特征提取的卷积层、用于图像尺度变换的几何变换层、用于加深图像特征提取的残差层三部分组成。在图像输入阶段经过kernel为7的卷积进行channel的加深,并得到图像的特征表示map,接着送入到几何变换层,所谓的几何变换层就是根据目标尺度T进行的图像的尺度上的简单转换过程,根据T来得到对应于T的尺度图像,在训练阶段这个T是由random_size函数随机产生的,详细的可以参看作者公布的源码。接着就是三层下采样,kernel的大小都是3,尺度都是0.5,然后在6层残差层下加深网络后送到上采样为2,最后得到T尺度的图像的彩色输出。需要强调的是在上下采样阶段,利用了U-Net的跳跃连接的思想对特征层进行了前后的联系进一步提高了图像转换中内容和结构的质量,下采样通过max pooling实现,上采样都过最近邻方式实现。
当训练完成,在训练阶段尺度T就可以人为的指定,从而得到需求下图像的尺度变换。
多尺度判别器
判别器采用的全卷积结构设计,整体结构如图4所示:
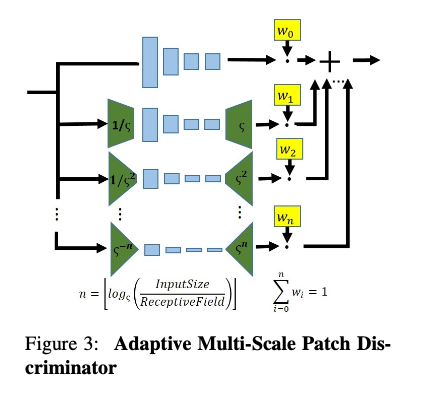
图4.InGAN中判别器的详细结构
提取出判别器一个尺度下结构进行分析,一个标准的网络由4个卷积层组成,一个卷积提取层,接着一个下采样层,再来一个常规卷积层,最后接上sigmoid激活函数下卷积层到[0,1]得分输出。这是一个尺度下的,对于多尺度,则将每一个尺度下的判别得分进行加权,最后得到最终的输出。至于这个多尺度是怎么得到的,这里就涉及到源码下的分析了,作者是通过设计scale_weight实现图像的多尺度的判别,设定的多尺度的上限为99,也就是在图像中进行了99个尺度的分布匹配。
实施细节
使用ADAM优化器和线性衰减学习率,batch size设定为1,对于循环一致损失的超参设定为0.1,在每次迭代中,T的参数都是随机采样的,从而导致不同的输出大小,形状和纵横比,在T的设计上在最初的时候是变化较小的,随着训练的进行,允许的变形范围在整个训练期间(10k次迭代)逐渐增大,直到最终覆盖整个所需范围。判别器和发生器中的谱归一化用于除最后一层以外的所有层,BatchNormalization在大多数conv块中使用,在实际事例中加入$[0, \frac{1}{255}]$范围内的均价噪声。
实验
在图像的重定向上,InGAN展示了合理而强大的转换效果:
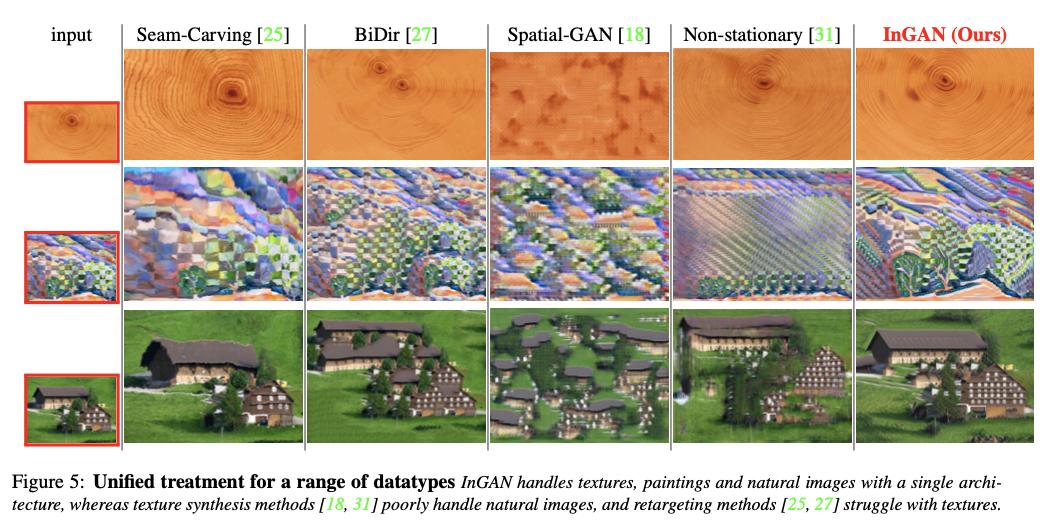
图5.InGAN与其它模型的图像重定向结构对比
在纹理合成上也展示了不错的结果:

图6.InGAN与其它模型的图像纹理合成对比
实验就一步做了消融实验,展示了循环一致和多尺度对抗的重要性:

图7.InGAN消融实验对比
总结
InGAN通过对单一图像的内部色块分布进行学习和分布匹配,在内部色块被学习到后可以实现图像的自然拉伸和重定向(可以产生大小,形状和纵横比明显不同的输出,包括非矩形输出图像)等任务,同时这个框架便可适用于这些任务而不需要再去更改。
但是InGAN每次只能训练一张图像,这可能有好处也有弊端。好处就是需要的训练集比较小,至于为什么一张图像就能训练网络,这也归功于文中随机变换尺度T的设计。然而每次只能训练一张图像,这样的话当需要处理另一张图像是还需要重新训练网络,这就增加了训练和时间成本了。能否通过设计普适性的预训练模型再通过具体的图像进行微调达到快速处理图像是可以进一步研究的方向。一旦训练成本降低,通过InGAN去扩充数据集,去处理数据集都是很不错的方法。
参考文献
[1] A. Buades, B. Coll, and J.-M. Morel. A non-local algorithm for image denoising. In CVPR, volume 2, pages 60–65, 2005. 1
[2] D. Simakov, Y. Caspi, E. Shechtman, and M. Irani. Summarizing visual data using bidirectional similarity. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2008. 1, 4, 5, 7
[3] Zhu J Y, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//Proceedings of the IEEE international conference on computer vision. 2017: 2223-2232.
[4] X. Mao, Q. Li, H. Xie, R. Y. K. Lau, and Z. Wang. Least squares generative adversarial networks. In Computer Vision (ICCV), IEEE International Conference on, 2017. 4










