空间自适应归一化下图像语义合成(论文解读)
深度学习在算力的推动下不断的发展,随着卷积层的堆叠,模型的层数是越来越深,理论上神经网络中的参数越多这样对数据的拟合和分布描述就能越细致。然而简单的堆叠卷积层又会引起梯度消失和过拟合的问题,伴随着解决方案下残差网络、归一化和非线性层被提出。本博客将对NVIDA近期的论文Semantic Image Synthesis with Spatially-Adaptive Normalization进行解读,这篇论文提出了适合保留语义信息的Spatially-Adaptive Normalization(空间自适应归一化),同时文章在实现细节上也很有参考意义。
论文引入
Batch Normalization (BN)在Inception v2[1]网络中被提出,它的设计之初是为了解决Internal Covariate Shift问题,也就是在训练过程中,隐层的输入分布老是变来变去。因为深层神经网络在做非线性变换前的激活输入值随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,这导致了训练收敛慢,也就是数据整体分布逐渐往非线性函数的取值区间的上下限两端靠近。所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。
我们知道数据白化,是对输入数据分布变换到0均值,单位方差的正态分布,这样会使神经网络较快收敛。如果这种”白化处理”作用在每一个隐层上,是不是可以稳定数据分布的同时加速收敛?这个问题的答案就是BN设计的根源了,BN就是通过一定的规范化手段,对于每个隐层神经元,把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布,使得非线性变换函数的输入值落入对输入比较敏感的区域,以此避免梯度消失问题。
掌握了Batch Normalization的作用后,其实后期演进的Instance Normalization[2]、Layer Normalization、Group Normalization、Weight Normalization在原理上的作用是相近的,都是为了稳定模型训练,只不过不同的归一化方法适用于不同的场合。比如在做图像翻译时,往往设置的BatchSize为1或者模型训练时BatchSize取值很小,这个时候Batch Normalization在对这批数据取均值和方差,而这批数据由于量不够,很难描述整体数据,此时就可以尝试使用Layer Normalization或者Group Normalization。
言归正传,回到本博客的主题Spatially-Adaptive Normalization(空间自适应归一化),已经有这么多好用的归一化方法了为啥还要Spatially-Adaptive Normalization呢?说清这个问题前,我们要来看一下Conditional Batch Normalization(CBN)[3],以图像和其标签为例,CBN就是通过BN将图片底层信息和标签信息结合,这样处理的好处就是让图像的标签(语义信息)指导图像的特征表达。这种标签信息往往是由热编码或者是低纬的向量通过感知层代替BN中的参数$\gamma$和$\beta$,如果这个标签信息是一张语义分割图呢?这种输入到感知层的方式将不能充分表达图像的语义信息了,此时Spatially-Adaptive Normalization便派上用场了,它正是处理这种标签信息是一张语义分割图时如何让图像的标签(语义信息)指导图像的特征表达。
总结一下论文的优势:
- 提出了Spatially-Adaptive Normalization,实现了给定输入语义布局的情况下合成逼真的图像。
- 可以根据输入图像和语义图指导合成语义信息下的图像。
Spatially-Adaptive Normalization
如果熟悉Conditional Batch Normalization的话,Spatially-Adaptive Normalization(SPADE)自然是很容易理解的,简单点说就是将Conditional Batch Normalization中的”标签”经过多层感知机换成了语义分割图经过卷积层而已。当然你要是不熟悉也没问题,我们接下来详细说明,在说明之前我们看一下Spatially-Adaptive Normalization的整体结构。
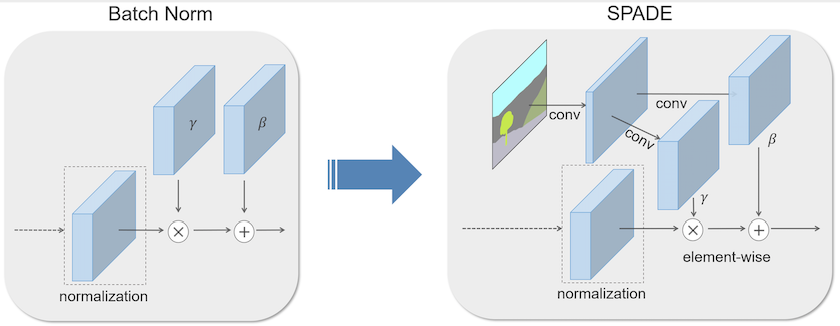
我们用$m \in \mathbb L^{H \times W}$表示语义分割图,其中$\mathbb L$表示语义标签的整数集,$H$ 和 $W$是图像的高度和宽度。论文的最终目的就是为了学习可以将输入分割掩模 $m$转换为逼真图像的模型结构。
设$h^i$表示给定一批 $N$ 个样本的深卷积网络的第$i$层激活层。设$C^i$是图层中通道的数量。设 $H^i$和$W^i$ 是各图层中激活层的高度和宽度。Spatially-Adaptive Normalization可以表示为:
\[\gamma_{c,y,x}^i(m) \frac{h_{n,c,y,x}^i-\mu_c^i}{\delta_c^i}+\beta_{c,y,x}^i(m)\]可以看出以通道方式进行归一化,其中$n \in N,c \in C_i,y \in H^i, x \in W^i$,$h_{n,c,y,x}^i$是归一化处理前的输入,$\mu_c^i$和$\delta_c^i$为通道$c$中输入的平均值和标准差:
\[\mu_c^i = \frac{1}{NH^iW^i}\sum_{n,y,x}h_{n,c,y,x}^i\] \[\delta_c^i = \sqrt{\frac{1}{NH^iW^i}\sum_{n,y,x}(h_{n,c,y,x}^i)^2-(\mu_c^i)^2}\]$\gamma_{c,y,x}^i(m)$和$\beta_{c,y,x}^i(m)$是Spatially-Adaptive Normalization学习参数,它们是通过语义分割图$m$经过卷积层得到的参数,此时的$\gamma_{c,y,x}^i(m)$和$\beta_{c,y,x}^i(m)$是包含语义分割图的语义信息的,同时也是语义分割图的feature map表示,这样学习到的参数将保留语义分割图的充分的语义信息,也实现了输入的归一化处理。
对于一般的归一化(BN、LN、IN、GN)只是对网络层中输入进行不同维度下求均值和标准差操作,例如Instance Normalization是对$H$ 和 $W$求均值和标准差,再进行归一化,这是用于图像的风格描述。假定我们对一个3通道的RGB图像求像素上的均值和标准差,不同风格的图像呈现的均值和方差是有差异的,比如艳丽的风格往往是像素特别丰富的,此时的图像像素均值自然是大的,阴暗风格对应的像素均值自然是小的。但是这仅仅是对输入的本身进行操作,这个过程没有语义的表示,而SPADE将语义分割图为输入提供了丰富的语义信息,这个可以实现输入下语义的传递和表达,这也是SPADE真正的意义所在。
语义图像的生成
介绍的SPADE只是实现语义图像合成的手段,并不是文章的最终目的,论文的目标是实现根据语义分割图实现语义图像的生成,也就是下面这个过程:

我们看一下完整的模型结构:

模型中的Image Encoder其实就是为了实现VAE[4]和GAN[5]结合的作用,目的是为语义图像的合成提供参考,也就是告诉模型按照语义分割指导合成的图像应该和我的整体风格类似。比如一批山水画作Image Encoder得到的特征隐变量通过KL映射到先验分布(高斯分布)上,通过采样根据语义分割图像的指导,解码生成包含语义信息的另一幅山水画。之所以加入VAE让图像编码的隐变量映射到先验分布上是为了在测试阶段可以通过随机采样实现语义图像的生成而不是再送入一张指导图像。
接下来我们将对模型细节进一步梳理,主要突出SPADE和SPADE ResBlk的设计介绍。
SPADE
这部分的结构如下:
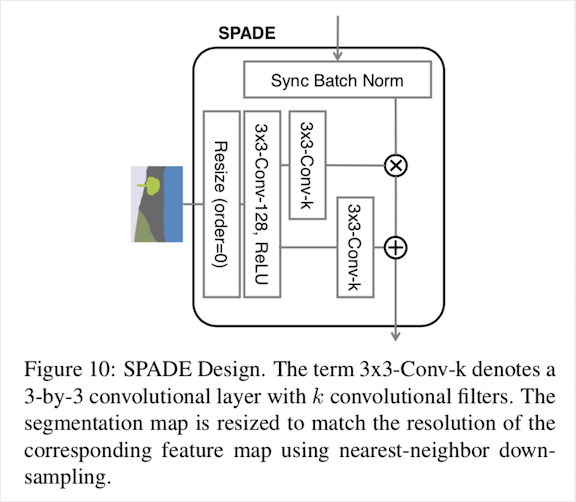
首先对语义分割图进行Resize,这步的作用是为了让语义分割图的输入尺寸和要进行归一化的输入尺寸保持一致,此处的Resize都是最近邻下采样实现。得到与输入相同尺寸map后,先通过一个$3 \times 3$卷积层得到128通道的语义分割图feature map,这一步主要是为了将原始的语义分割图3通道进行升维到128通道,接着就是分别经过两个$3 \times 3$卷积层得到对应的$\gamma$和$\beta$,此处的$k$要根据实际而定。得到$\gamma$和$\beta$后就可以和输入(已经和均值和标准差处理过)进行操作。在源码中,在SPADE内部就进行了一个残差操作,图中没有画出而已,结合分析,我们用tensorflow对SPADE进行实现:
def spade(segmap, x_init, channels, use_bias=True, sn=False, scope='spade'):
with tf.variable_scope(scope):
x = param_free_norm(x_init) # 进行均值,标准差计算,(x - x_mean) / x_std
_, x_h, x_w, _ = x_init.get_shape().as_list()
_, segmap_h, segmap_w, _ = segmap.get_shape().as_list()
factor_h = segmap_h // x_h # 确定下采样的比例
factor_w = segmap_w // x_w
segmap_down = down_sample(segmap, factor_h, factor_w) # 最近邻下采样
# 第一步卷积处理
segmap_down = conv(segmap_down, channels=128, kernel=5, stride=1,
pad=2, use_bias=use_bias, sn=sn,scope='conv_128')
segmap_down = relu(segmap_down)
# 两个卷积得到segmap_gamma和segmap_beta
segmap_gamma = conv(segmap_down, channels=channels, kernel=5, stride=1,
pad=2, use_bias=use_bias, sn=sn,scope='conv_gamma')
segmap_beta = conv(segmap_down, channels=channels, kernel=5, stride=1,
pad=2, use_bias=use_bias, sn=sn,scope='conv_beta')
# 引入残差
x = x * (1 + segmap_gamma) + segmap_beta
return x
def param_free_norm(x, epsilon=1e-5):
x_mean, x_var = tf.nn.moments(x, axes=[1, 2], keep_dims=True)
x_std = tf.sqrt(x_var + epsilon)
return (x - x_mean) / x_std
def down_sample(x, scale_factor_h, scale_factor_w):
_, h, w, _ = x.get_shape().as_list()
new_size = [h // scale_factor_h, w // scale_factor_w]
return tf.image.resize_nearest_neighbor(x, size=new_size)
SPADE ResBlk
我们再来看SPADE ResBlk的结构:
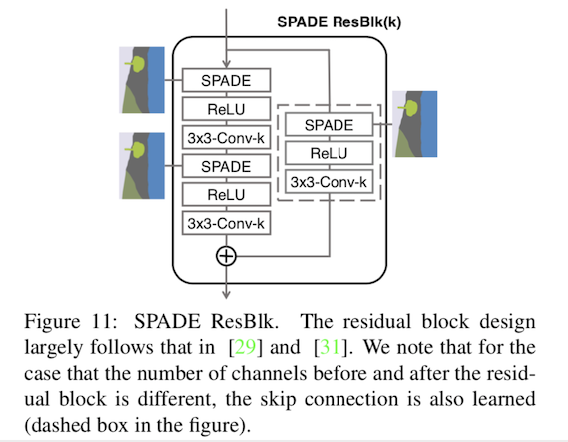
它是由主路下两个SPADE和残差分路SPADE构成,分路的SPADE主要是为了保证残差块之前和之后的通道数量不同的情况下的操作(这步主要发生在channel变化的阶段,如生成器中1024到512的过程),我们用tensorflow实现SPADE ResBlk:
def spade_resblock(segmap, x_init, channels, use_bias=True, sn=False, scope='spade_resblock'):
channel_in = x_init.get_shape().as_list()[-1]
channel_middle = min(channel_in, channels) # 由于是生成阶段,channel是逐渐变小的
with tf.variable_scope(scope):
x = spade(segmap, x_init, channel_in, use_bias=use_bias, sn=False, scope='spade_1')
x = lrelu(x, 0.2)
x = conv(x, channels=channel_middle, kernel=3, stride=1,
pad=1, use_bias=use_bias, sn=sn, scope='conv_1')
x = spade(segmap, x, channels=channel_middle, use_bias=use_bias,
sn=False, scope='spade_2')
x = lrelu(x, 0.2)
x = conv(x, channels=channels, kernel=3, stride=1, pad=1,
use_bias=use_bias, sn=sn, scope='conv_2')
if channel_in != channels:
x_init = spade(segmap, x_init, channels=channel_in, use_bias=use_bias,
sn=False, scope='spade_shortcut')
x_init = conv(x_init, channels=channels, kernel=1, stride=1,
use_bias=False, sn=sn, scope='conv_shortcut')
return x + x_init
整个生成器的架构就可以由SPADE ResBlk进行设计,判别器首先将语义分割图和真实(生成)进行concat再逐步下采样,由于这是图像翻译的过程,默认情况下batch size取1,所以在判别器下不适合用BN,而使用的IN作为归一化处理(个人感觉LN得到的效果应该也会不错的)。图像编码器的架构是个下采样过程,也是采用IN,输出为均值和方差,用于拟合先验分布(高斯分布)。
论文涉及到训练中的损失函数主要是生成对抗损失和拟合先验分布的KL loss,对抗损失默认采用的是hinge loss,还涉及到特征匹配损失,生成器和判别器的正则化损失以及衡量生成和真实图像的VGG loss,感兴趣的可以阅读源码进一步了解,[Pytorch版本]、[tensorflow版本]。
实验
实施细节上,采用Spectral Norm [6]应用于生成器和判别器中的所有层。 生成器和判别器的学习率分别设置为0.0001 和 0.0004。优化器使用 ADAM 并设置$\beta_1 = 0$ ,$\beta_2= 0.999$。分别在COCO-Stuff、ADE20K、ADE20K-outdoor、Cityscapes 、FlickrLandscapes数据集上进行实验。
在定性上,结果还是很有说服力的:

在定量上也展示了优势:

在模型参数上也有一定优势:
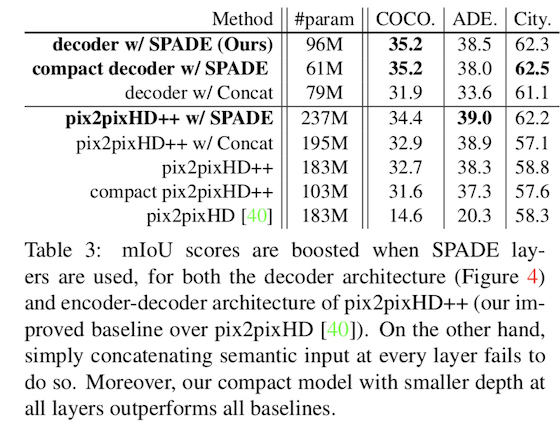
总结
论文提出了Spatially-Adaptive Normalization(空间自适应归一化),该方法对Conditional Batch Normalization(条件批归一化)进行了改进,将标签信息换成了语义分割图,通过卷积层代替多层感知层为图像合成提供了丰富的语义信息。同时这种转换也不仅仅适用于语义分割图,甚至可以在语音和视频中得到改进和发展。
参考文献
[1] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning (ICML), 2015.
[2] D. Ulyanov, A. Vedaldi, and V. Lempitsky. Instance nor- malization: The missing ingredient for fast stylization. arxiv 2016. arXiv preprint arXiv:1607.08022, 2016.
[3] V. Dumoulin, J. Shlens, and M. Kudlur. A learned repre- sentation for artistic style. In International Conference on Learning Representations (ICLR), 2016.
[4] Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013.
[5] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.
[6] T. Miyato, T. Kataoka, M. Koyama, and Y. Yoshida. Spec-tral normalization for generative adversarial networks. In In-ternational Conference on Learning Representations (ICLR), 2018.










