VDB论文解读
生成对抗网络中判别器在二分类游戏上表现了强大的区分能力,RSGAN使用相对判别器将真假样本混合利用 “图灵测试”的思想削弱了判别器的能力,T-GANs将RSGAN一般化到其它GAN模型下,判别器得到限制在整体上平衡了生成器和判别器, 可以使GAN训练上更加稳定。VDB通过对判别器加上互信息瓶颈限制判别器的能力。
论文引入
GAN存在两大固有问题,一个是生成上多样性不足;另一个就是当判别器训练到最优时,生成器的梯度消失。造成梯度消失的原因在于生成样本和真实样本在分布上是不交叠的, WGAN提出可以通过加入噪声来强制产生交叠,但是如何控制噪声加入以及能否保证交叠都是存在问题的。 WGAN以及它的改进虽然在GAN训练中稳定性上提高了,但是对于样本真假的二分类判别上,判别器展现了过于强大的能力,这样打破了对抗上的平衡问题, 最终还是造成训练阶段的不稳定(不平衡,生成质量提不上去)。
RSGAN提出了采用相对判别器通过区分真假样本混合在一起判断真假,这样判别器不再是判断真或假,还要在一堆样本下将真假样本分开。这样对于判别器的要求提高了, 难度上来后自然会进一步平衡训练,关于RSGAN的进一步理解可参看这篇博客。T-GANs更是进一步将RSGAN一般化, 让RSGAN中的混合真假样本的思想得到充分应用,具体了解,可参看这篇博客。
VARIATIONAL DISCRIMINATOR BOTTLENECK :IMPROVING IMITATION LEARNING , INVERSE RL, AND GANS BY CONSTRAINING INFORMATION FLOW (变分判别器瓶颈)是我们今天要来读的文章。文章对于判别器通过对互信息加上限制,来削弱判别器的能力,从而平衡网络的训练。这种对判别器互信息限制, 不仅可以用在GAN的训练上,对于模仿学习和逆强化学习都有很大的提高。由于我更加关注VDB在GAN上的应用,所以在模仿学习和你强化学习我们将做简短介绍, 把重点放在VDB在GAN上的作用。
在开启正文前,我们一起看一下互信息瓶颈限制在监督学习上的正则作用,这个思想在16年被Alemi提出,原文叫Deep variational information bottleneck。 我们有数据集${ x_i,y_i }$,其中$x_i$为数据样本,$y_i$为对应的标签,通过最大似然估计优化模型:
\[\begin{equation} \min_q \mathbb E_{x,y \sim p(x,y)} [-log q(y \vert x)] \end{equation}\]这种最大似然估计方法往往会造成过拟合的现象,这时候就需要一定的正则化,变分互信息瓶颈则是鼓励模型仅关注最具辨别力的特征,从而对模型做一定的限制。 为了实现这种信息瓶颈,需要引入编码器对样本特征先做提取$E(z \vert x)$将样本编码到特征空间$z$,通过对样本$x$和特征空间$z$的互信息$I(X,Z)$ 做限制,即$I(X,Z) \leq I_c$,则正则化目标:
\[\begin{equation} J(q,E) = min_{q,E} \mathbb E_{x,y \sim p(x,y)} [ \mathbb E_{z \sim E(z \vert x)} [-log q(y \vert z)]] \\ s.t. I(x,Z) \leq I_c \end{equation}\]此时最大似然估计就是对模型$q(y \vert z)$操作的,实现将特征空间$z$到标签$y$,互信息定义为:
\[\begin{equation} I(X,Z) = \int p(x,z) log \frac{p(x,z)}{p(x)p(z)} dx dz = \int p(x) E(z \vert x) log \frac{E(z \vert x)}{p(z)} dx dz \end{equation}\]这里的$p(x)$为数据样本的分布,$p(x,z) = p(x) E(z \vert x)$,计算分布$p(z) = \int p(x) E(z \vert x) dx$是困难的,$p(z)$是数据编码得到的, 这个分布是很难刻画的,但是可以使用边际的近似$r(z)$可以获得变分下界。取$KL[p(z) \Vert r(z)] = \int p(z)logp(z) - \int p(z)log r(z) \geq 0$ 此时$\int p(z)logp(z) \geq \int p(z)log r(z)$,$I(X,Z)$可以表示为:
\[\begin{equation} I(X,Z) \leq \int p(x) E(z \vert x) log \frac{E(z \vert x)}{r(z)} dx dz = \mathbb E_{x \sim p(x)} [KL[E(z \vert x) \Vert r(z)]] \end{equation}\]这提供了正则化的上届,$\tilde J(q,E) \geq J(q,E)$。
\[\begin{equation} \tilde J(q,E) = min_{q,E} \mathbb E_{x,y \sim p(x,y)} [ \mathbb E_{z \sim E(z \vert x)} [-log q(y \vert z)]] \\ s.t. \mathbb E_{x \sim p(x)} [KL[E(z \vert x) \Vert r(z)]] \leq I_c \end{equation}\]优化的时候可以采取拉格朗日系数$\beta$。我们从整体上分析一下这个互信息的瓶颈限制,我们知道互信息反应的是两个变量的相关程度,而我们得到的特征空间$z$ 是由$x$编码得到的,理论上已知$x$就可确定$z$,$x$和$z$是完全相关的,也就是$x$和$z$的互信息是较大的,而现在限制了互信息的值,这样就切断了一部分$x$和$z$ 的相关性,保留的相关性是$x$和$z$最具辨别力的特征,而其它相关性较低的特征部分将被限制掉,从而使得模型不至于过度学习,从而实现正则化的思想。
VDB正是把这个用在监督学习的正则思想用到了判别器上,从而在GAN、模仿学习和逆强化学习上都取得了不小的提升,总结一下VDB的优势:
- 判别器信息瓶颈是对抗性学习的自适应随机正则化方法,可显着提高各种不同应用领域的性能
- 在GAN、模仿学习和逆强化学习上取得性能上的改进
VDB在GAN中的实现
VDB其实是在Deep variational information bottleneck的基础上将互信息思想引入到判别器下,如果上面描述的互信息瓶颈读懂的话,这一块将很好理解。 对于传统GAN,我们先定义下各个变量(保持和原文一致)。真实数据样本分布$p^*(x)$,生成样本分布$G(x)$,判别器为$D$,生成器为$G$,目标函数为:
\[\begin{equation} \max_G \min_D \mathbb E_{x \sim p^*(x)} [-log(D(x))] + \mathbb E_{x \sim G(x)} [-log(1-D(x))] \end{equation}\]类似于Deep variational information bottleneck,文章也是先对数据样本做了Encoder,经数据编码到特征空间下,这样一来降低了数据的维度, 同时将真假样本都做低维映射,更加可能实现一定的交叠,当然这个不是文章的重点,文章的重点还是为了在互信息上实行瓶颈限制。将数据编码得到的$z$ 和数据$x$的互信息做瓶颈限制,我们先看目标函数,再来解释为什么做了瓶颈限制可以降低判别器的能力。
\[\begin{equation} J(D,E) = min_{D,E} \mathbb E_{x \sim p^*(x)}[\mathbb E_{z \sim E(z \vert x)} [-log(D(z))]] + \mathbb E_{x \sim G(x)} [\mathbb E_{z \sim E(z \vert x)} [-log(1-D(z))]] \\ s.t. \mathbb E_{x \sim \tilde p(x)} [KL[E(z \vert x) \Vert r(z)]] \leq I_c \end{equation}\]这里强调一下$\tilde p = \frac{1}{2} p^* + \frac{1}{2} G$,这个我们待会再进一步分析,同样可以通过引入拉格朗日系数优化目标函数:
\[\begin{equation} J(D,E) = min_{D,E} \max_{\beta \geq 0} \mathbb E_{x \sim p^*(x)}[\mathbb E_{z \sim E(z \vert x)} [-log(D(z))]] + \mathbb E_{x \sim G(x)} [\mathbb E_{z \sim E(z \vert x)} [-log(1-D(z))]] \\ +s.t. \beta(\mathbb E_{x \sim \tilde p(x)} [KL[E(z \vert x) \Vert r(z)]] - I_c) \end{equation}\]我们分析一下限制互信息瓶颈在GAN中起到的作用,同样的互信息是样本$x$和它经过编码得到的特征空间$z$。互信息表示变量间的相关程度,通过限制$x$和$z$ 的相关性,对于很具有辨识性的特征,判别器将可以区分真假,但是经过信息瓶颈限制把样本和特征空间相关性不足的特征限制住,这样判别器就增加了区分样本真假的难度。 判别器在这个二分类游戏下只能通过相关性很强的特征来判断真假,对于限制条件下$\tilde p = \frac{1}{2} p^* + \frac{1}{2} G$, 这个的作用是对整体样本的互信息都进行限制,这样真假样本都进行了混淆,判别器判断难度提高,游戏得到进一步平衡。
文章通过实验进一步说明了判别器加入信息瓶颈的作用,通过对两个不同的高斯分布进行区别,左侧认为是假(判为0),右侧认为是真(判为1), 经过信息瓶颈限制$I_c$的调整,得到的结果如下图:
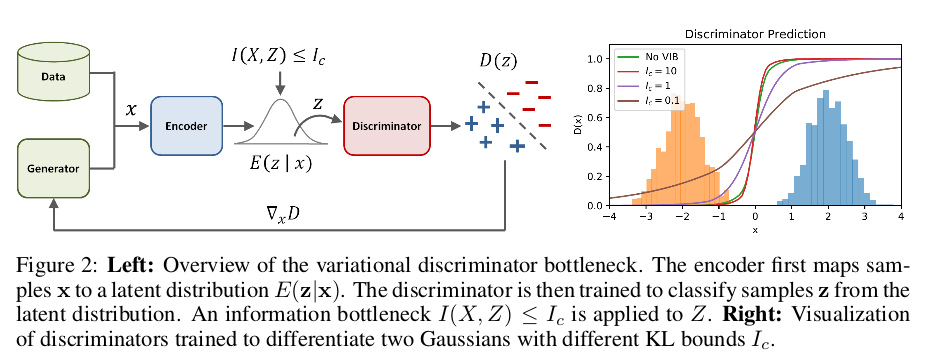
我们知道,在二分类下信息熵最小是1bit(当两个事件等概率发生时),由于$x$和$z$是完全相关,我们可以理解理想状态此时的互信息最小是1bit, 当我们不断减小瓶颈$I_c$的值,上图中由10降到0.1,这个过程中判别器区分两个分布的界限越来越弱,达到了限制判别器能力的效果。
对于网络的优化,主要是对$\beta$的更新上:
\[\begin{equation} D,E \gets \arg \min_{D,E} \mathcal L(D,E,\beta) \\ \beta \gets max(0, \beta + \alpha_{\beta} (\mathbb E_{x \sim \tilde p(x)} [KL[E(z \vert x) \Vert r(z)]] - I_c)) \end{equation}\]这个互信息瓶颈还可以用在模范学习和逆强化学习上,都取得了一定的改进,感兴趣的可以查看原文进一步了解。
实验
VDB在GAN中的应用实验,作者对cifar10做了各个模型的FID定量对比,为了改善VDB在GAN上的性能,作者在VDB在GAN中加入了梯度惩罚,命名为VGAN-GP。 这样可谓是又进一步限制了判别器,反正实验效果是有所提升,可以猜测作者用到的GAN的损失函数肯定是建立在WGAN基础上的了,文中说了代码即将公布, 没看到源码前只能猜测一下。
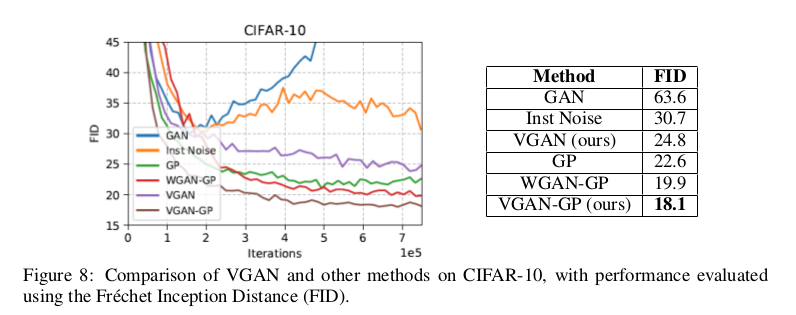
不过通过后文实验做到了$1024 \times 1024$可以看出,作者所在的实验室一定不简单,跑得动1024的图,只能表示一下敬意。

最后,来看一下作者在Youtube上展示的视频Demo(观看需要翻墙)
总结
文章提出了变判别器瓶颈,这是一种用于对抗学习的一般正则化技术。实验表明,VDB广泛适用于各种领域,并且在许多具有挑战性的任务方面比以前的技术产生了显着的改进。 通过对判别器加入信息瓶颈,限制了判别器的能力,使得对抗中保持平衡,提高了训练的稳定性,这中正则化思想可以在各类GAN模型下适用,后续还要对VDB 做进一步实验上的分析。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










