GANomaly论文解读
异常检测(Anomaly Detection)是计算机视觉中的一个经典问题,生活中大部分的数据是正常数据,有很少一部分属于异常数据,在很少的异常下如何检测出异常 是一个困难的课题,甚至不知道什么是异常,只知道不属于正常的就算异常的话又如何检测异常呢?GANomaly 便是可以实现在毫无异常样本训练下对异常样本做检测,我们一起来读一下。
论文引入
在计算机视觉上大部分的检测任务的前提是需要大量的标记数据做训练,这虽然在成本上耗费巨大,但是在实验效果上确实有很大的突破,目前的目标检测技术 已经上升到近乎实时检测的效果了,背后的人力和成本也是可想而知的。在庞大的目标检测背景下,异常检测算是一个特立独行的分支,虽然只是判断正常和异常 两种情况(二分类问题),但是往往异常样本特别的少,如果从特征提取上区分正常和异常的话,由于训练样本过少或者说是训练样本比例太不平衡(正常样本特别多) 往往会导致实验结果上不尽如人意。
异常检测的发展在深度学习的浪潮下得到了很快的发展,基于CNN,RNN、LSTM技术上已经取得了一定的成效。随着GAN的提出,对抗的思想越来越引人注意, 利用GAN做异常检测的文章在实验上有了一定的突破,从AnoGAN学习到正常样本的分布,一旦送入异常样本数据发生改变从而检测出异常, 这种方法的局限性很强,往往也会带来计算成本的昂贵(需要严格的控制先验分布z)。在此基础上,为了找到更好用作生成的先验分布z,在AnoGAN的基础上提出了 Efficient-GAN-Anomaly同样由于做个一次重新映射导致计算成本上也是庞大的。
GANomaly算是在前两篇文章的基础上做了一次突破,不在比较图像分布了,而是转眼到图像编码的潜在空间下进行对比。对于正常的数据编码解码再编码得到的 潜在空间和第一次编码得到的潜在空间差距不会特别大。但是,在正常样本训练下的AE用作从未见过的异常样本编码解码时,再经历两次编码过程下往往 潜在空间差距是大的,当两次编码得到的潜在空间差距大于一定阈值的时候,我们就判定样本是异常样本,这就是GANomaly的思路。我们以此对比一下以GAN 为发展下的异常检测模型,模型结果如下,上述已对其做了一定的分析。
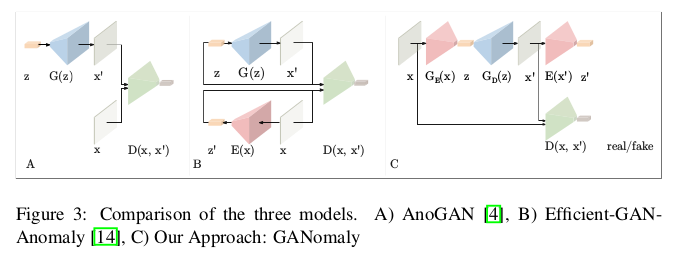
GANomaly的优势总结一下:
- 半监督异常检测:编码器-解码器-编码器流水线内的新型对抗自动编码器,捕获图像和潜在向量空间内的训练数据分布
- 功效:一种有效且新颖的异常检测方法,可在统计和计算上提供更好的性能
GANomaly模型
我们还是先看一下模型框架:
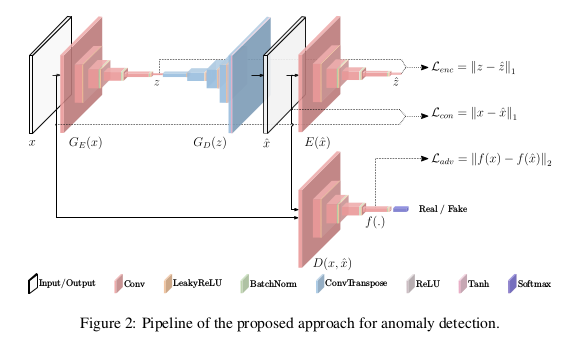
GANomaly模型框架是蛮清晰的,整个框架由三部分组成:$G_E(x),G_D(z)$统称为生成网络,可以看成是第一部分。这一部分由编码器$G_E(x)$和解码器 $G_D(z)$构成,对于送入数据$x$经过编码器$G_E(x)$得到潜在向量$z$,$z$经过解码器$G_D(z)$得到$x$的重构数据$\hat{x}$。模型的第二部分就是 判别器D,对于原始图像$x$判为真,重构图像$\hat{x}$判为假,从而不断优化重构图像与原始图像的差距,理想情况下重构图像与原始图像无异。 模型的第三部分是对重构图像$\hat{x}$再做编码的编码器$E(\hat{x})$得到重构图像编码的潜在变量$\hat{z}$。
在训练阶段,整个模型均是通过正常样本做训练。也就是编码器$G_E(x)$,解码器$G_D(z)$和重构编码器$E(\hat{x})$,都是适用于正常样本的。当模型在 测试阶段接受到一个异常样本,此时模型的编码器,解码器将不适用于异常样本,此时得到的编码后潜在变量$z$和重构编码器得到的潜在变量$\hat{z}$ 的差距是大的。我们规定这个差距是一个分值$\mathcal A(x) = \Vert G_E(x) - E(G(x)) \Vert_1$,通过设定阈值$\phi$,一旦$\mathcal A(x) > \phi$ 模型就认定送入的样本$x$是异常数据。
网络损失
对于模型的优化,全是通过正常样本实现的,网络损失也可分为三部分。标准GAN的损失大家相比都很清楚了,这里不重复写。对于第一部分的生成网络下, 文章给定了一个重构误差损失,用于在像素层面上减小原始图像和重构图像的差距。
\[\mathcal L_{con} = \mathbb E_{x \sim p_X} \Vert x - G(x) \Vert_1\]对于第二部分判别器下,设置了一个特征匹配误差,用于在图像特征层方面做优化,这部分损失其实已经在很多文章中都用到过。
\[\mathcal L_{adv} = \mathbb E_{x \sim p_X} \Vert f(x) - f(G(x)) \Vert_2\]对于第三部分重构图像编码得到的潜在变量$\hat{z}$,这部分对于正常数据而言,希望得到的$\hat{z}$与原始数据直接编码得到的$z$无差别最好, 也就是对于最好的得分判断,对于正常数据而言理想状态下希望$\mathcal A(x) = \Vert G_E(x) - E(G(x)) \Vert_1 = 0$。当然这是最理想的状态, 但是对于正常数据还是希望$\mathcal A(x)$越小越好,所以引入了一个潜在变量间的误差优化。
\[\mathcal L_{enc} = \mathbb E_{x \sim p_X} \Vert G_E(x) - E(G(\hat{x}))\]训练过程中只有正例样本参与,模型只对正例样本可以做到较好的编码解码,所以送入负例样本在编解码下会出现编码得到的潜在变量差异大从而使得差距分值 $\mathcal A(x)$大,判断为异常。对于模型,整个损失函数可以表示为:
\[\mathcal L = \omega_{adv} \mathcal L_{adv} + \omega_{con} \mathcal L_{con} + \omega_{enc} \mathcal L_{enc}\]这里的$\omega_{adv},\omega_{con},\omega_{enc}$是调节各损失的参数,可以根据具体实验设置。
模型测试
模型测试过程中以正负样例$\hat{D}$混合输入,对于测试样本下的得分S可记为$S = \lbrace s_i: \mathcal A(\hat{x_i}),\hat{x_i} \in \hat{D} \rbrace$ 具体的判断异常分数进行一个归一化处理将其整合到[0,1]之间。
\[s_i^, = \frac{s_i - min(S)}{max(S) - min(S)}\]这里的$s_i^,$就是最终的异常得分,对于正常样本理论上希望$s_i^, = 0$,对于异常样本理论上希望$s_i^, = 1$。需要一个阈值$\phi$来衡量这个标准, 经过源码分析一般的$\phi = 0.2$可以根据实际项目需要对$\phi$做调整。
GANomaly实验
实验在MNIST,CIFAR10上选取部分类别做正样本,选取一些类别作异常样本,测试模型是否能够检测出异常样本并给出准确率。文章的衡量标准是以AUC为判断。 实验对比了三种以GAN做异常检测的模型以及VAE的结果,通过AUC分析可以看出GANomaly取得了不错的优势。
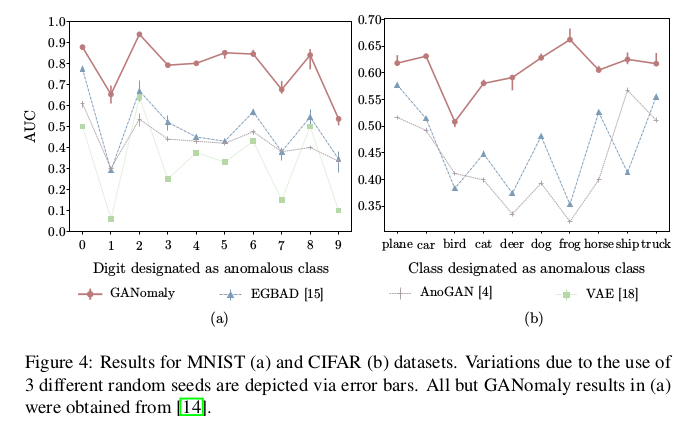
实验还对大件行李异常数据集(University Baggage Anomaly Dataset - (UBA))做了实验,数据集包括230275个图像块,图像从完整的X射线图像中提取, 异常类别(122803)有3个子类 - 刀(63,496),枪(45,855)和枪组件(13,452),对于另一个数据集选择了枪械检测(FFOB)。
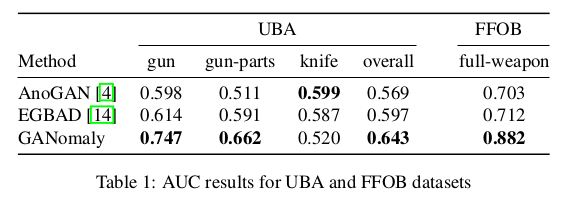
对于潜在变量的选取,以及超参的确定也通过实验选取:
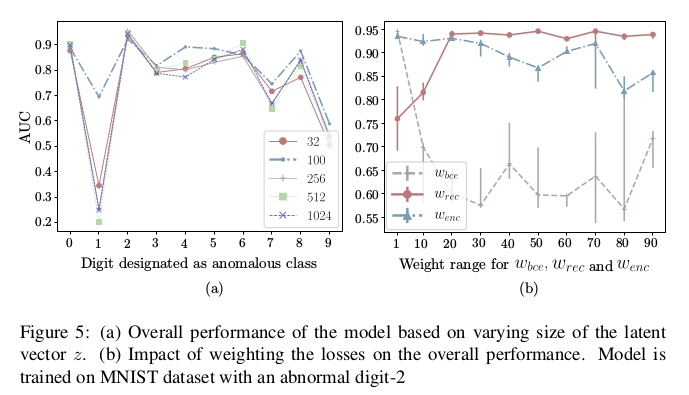
最后来看一下正常样本和异常样本重构的对比,可以看出异常样本在重构上已经和原始有了较大的差别了,所以编码得到的潜在变量自然会产生差异, 从而判断出异常。
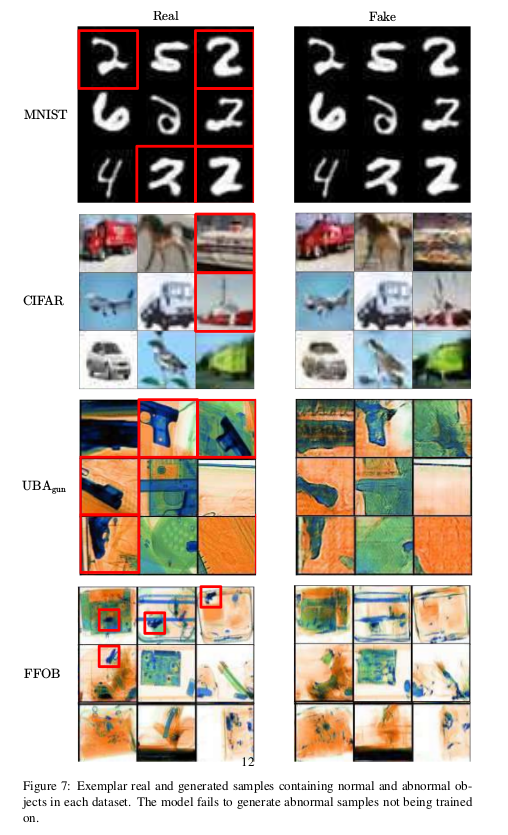
总结
GANomaly以编码器-解码器-编码器设计模型,通过对比编码得到的潜在变量和重构编码得到的潜在变量差异从而判断是否为异常样本。文章实现了在无异常 样本训练模型的情况下实现了异常的检测,对于很多场景都有很强的实际应用意义。个人感觉文章对于异常分数的计算和判断可再进一步优化,从而实现更好的异常检测效果。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










