Latent Constraints论文解读
有条件训练数据集做生成任务需要庞大的标签数据,CGAN和CVAE的思想可以较好的实现条件生成,除了本身的弊端之外。这两种思想训练的模型一旦加入 新的标签数据再来做生成的话,往往需要重新训练模型,这个的代价是很高的。Latent Constraints 在保持原无条件生成网络不变的情况下通过训练潜在变量实现有条件生成,我们一起来读一下。
论文引入
很多文章都已经证明深度生成神经网络在复杂数据分布的条件和无条件建模方面都是有效的。对图像和音频等复杂数据进行生成建模是机器学习中长期存在的挑战, 虽然无条件抽样是一个有趣的技术问题,但它本身的实际利益可能有限:如果需要一个非特定的图像(或声音,歌曲,文档等),人们可以简单地在网络上庞大媒体 数据库下随意抽取一些数据做训练。但是这种方法可能不适用于条件采样(生成数据以匹配一组用户指定的属性),因为随着指定的属性越来越多, 从数据库中提取令人满意的示例的可能性就越小。人们可能还想修改对象的某些属性,同时保留其核心身份。这些是创造性应用中的关键任务,具有很大的意义。
条件生成可以实现交互式控制,让用户可以根据自己的需求实现有条件的生成,条件生成相比于无条件生成上意义是较大的。但是训练也是昂贵的, 往往需要打好标签的数据集来训练模型,一旦数据集更新或者增加了标签数据相应的模型也需要重新训练,这个的代价会更高。
CGAN和CVAE思想是在深度网络下表现较好的两个生成模型,但是除了CVAE和CGAN固有的问题之外,它们的训练对数据集的要求很高,同时一旦数据集的标签 数据增加模型也需要重新训练,这个问题就是上面我们提到的昂贵的成本。如何能在保持条件生成的基础上,解决好上述问题对于条件生成的发展是有很大推动的。 Latent Constraints就是在无监督下训练好生成模型,然后通过改变潜在变量实现有条件的生成,虽然需要带标签的数据集但是可以实现在新增标签数据下 在不重新训练生成模型的前提下实现条件生成。
Latent Constraints的整体思路就是先训练好一个VAE模型,通过有标签信息参与的情况下将先验分布映射到较好的后验分布上,再进一步Decoder出这个 条件下的数据,从而实现无监督模型下有条件生成。总结一下Latent Constraints的优势:
- 实现了从无条件模型中有条件地生成
- 一定程度上解决了VAE生成图像上模糊的问题
- 减小了新增标签数据再训练的计算成本
权衡VAE重构和生成
VAE在图像生成上展示了一定的优势,但是由标准VAE生成的图像往往是模糊的,已经有很多研究在改进VAE生成上的模糊但是通过单纯的在VAE基础上改进的话 会发现当控制VAE中的高斯方差$\sigma$的大小以最大化ELBO会造成重构和生成出的样本一个清晰一个很糟。Latent Constraints通过实验找到了当 $\sigma = 0.1$的时候此时VAE的重建效果最好。而我们知道在标准的VAE下$\sigma = 1$,当$\sigma = 0.1$的时候也就是方差变小了,此时整个 高斯分布下采样得到的结果将会更加集中,而将后验分布$q(z \vert x)$通过KL拉向先验分布$p(z)$的话,此时的$p(z)$的采样在表示后验$q(z \vert x)$ 的紧密性上是不充足的,这样就会造成采样生成上的结果很糟糕。但是$\sigma$较小的时候,对于数据的重建效果是好的,我们可以通过实验对比进一步感受一下:

我们可以看到,当$\sigma = 1$的时候重构和采样生成的结果都是模糊的,当我们改变$\sigma$到0.1的时候,此时重构出的图像是清晰的但是对应采样 生成的图像是糟糕的,如何改进采样生成的结果呢?文章中在模型中加上了“Realism”判别器。
“Realism”判别器
“Realism”判别器的作用就是为了提高在$\sigma = 0.1$的时候采样生成的结果,它的基本原理就是将需要采样的先验分布$p(z)$通过一个生成器G将$p(z)$ 映射到后验分布$q(z \vert x)$得到一个新的潜在变量$z’$,此时的$z’$就可以较好的表示后验分布$q(z \vert x)$,我们知道后验分布$q(z \vert x)$ 做重构出的结果是清晰的,此时在先验分布$p(z)$下做采样经过映射接近$q(z \vert x)$后再生成出的结果应该和重构得到的结果相近,也是清晰的, 这个过程就是“Realism”判别器的目的。
当然我们的目的是实现由$p(z)$到$q(z \vert x)$的映射,这个过程采用的是GAN的思想。输入$p(z)$经过生成器$G(z)$得到结果$z’$,将$z’$和 真实后验分布$q(z \vert x)$送到“Realism”判别器判别真假从而实现对抗共同进步。对于真实的后验分布$q(z \vert x)$是真实的给予的标签$c=1$ 对应的$\mathcal L_{c=1} = -log(D(z))$,生成的$z’$和先验分布$p(z)$为假即标签$c=0$对应的$\mathcal L_{c=1} = -(1 - log(D(Z)))$。 这样最后的“Realism”判别器的损失为:
\[\mathcal L_{D(z)} = \mathbb E_{z \sim q(z \vert x)}[\mathcal L_{c=1}(z)] + \mathbb E_{z \sim p(z)}[\mathcal L_{c=0}(z)] + \mathbb E_{z \sim G(p(z))}[\mathcal L_{c=0}(z)]\]判别器的损失知道了,生成器的损失和其对应,但是文中为了缓解GAN训练上的多样性问题引入了正则化项$\mathcal L_{dist}(z’,z) = \frac{1}{\bar{\sigma_z^2}} log(1 + (z’ - z)^2)$ 其中$\bar{\sigma_z} = \frac{1}{N} \sum_n \sigma_z(x_n)$,此时的生成器G的损失函数:
\[\mathcal L_{G(z)} = \mathbb E_{z \sim p(z)}[\mathcal L_{c=1}(G(z)) + \lambda_{dist} \mathcal L_{dist}(G(z),z)]\]通过“Realism”判别器的引入使得从先验分布$p(z)$下采样通过映射再生成的结果上的到了很大的提高,具体实验结果如下:

可以看出相比较直接从先验中采样生成,映射之后的生成结果要好的多。
属性判别器
上述的所有讨论都还是在做无条件生成,而文章的重点是在有条件的生成上,怎么是现在已经预训练好的生成模型上实现有条件生成呢?这就是文章引入的 属性判别器的作用了。属性判别器其实很简单,就是在先验分布$p(z)$映射的过程中将上述的生成器加入数据标签做有条件的映射。
将先验分布$p(z)$作为输入送到属性生成器$G(z,y)$下生成新的潜在变量$z’$,此时的$z’$是包含了标签信息的潜在变量用它来Decoder将会得到标签$y$ 对应的图像。这个$z’$怎么优化呢?又是GAN的一套理论了,将数据标签$y$对应的图像经过Encoder得到的后验分布$q(z \vert x)$作为真实样本,生成的 $z’$和先验分布$p(z)$作为假样本在属性判别器下判断真假从而在博弈下,此时的$z’$将和$y$标签对应的后验分布$q(z \vert x)$相近,从而实现了 先验分布$p(z)$在标签$y$下映射为潜在变量$z’$再Decoder成标签$y$对应的图像,从而实现了有条件的生成。
这一块的损失优化和“Realism”判别器的优化基本相同只不过是嵌入了标签$y$而已,其实属性判别器就是CGAN的思想。
Latent Constraints模型
通过上述的分析,我们一起看一下Latent Constraints的模型结构:
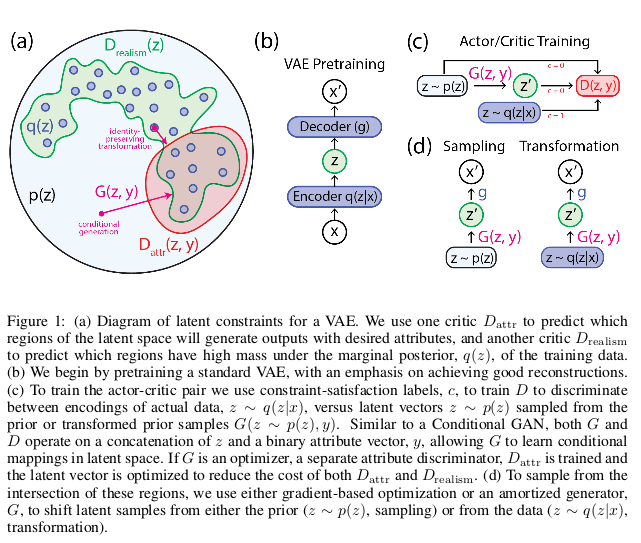
这个图是将各个部分分开画的,先预训练一个VAE,然后通过生成器的映射将$p(z)$映射到潜在变量$z’$下从而再Decoder得到条件生成的数据。具体生成上 实验上,在先验分布$p(z)$下采样再给予标签$y$即可生成对应的条件下的图像。实验展示如下:

有趣的是正则项的引入在实验上并没有得到特别好的实验对比,但是正则项在改进上是可取的:
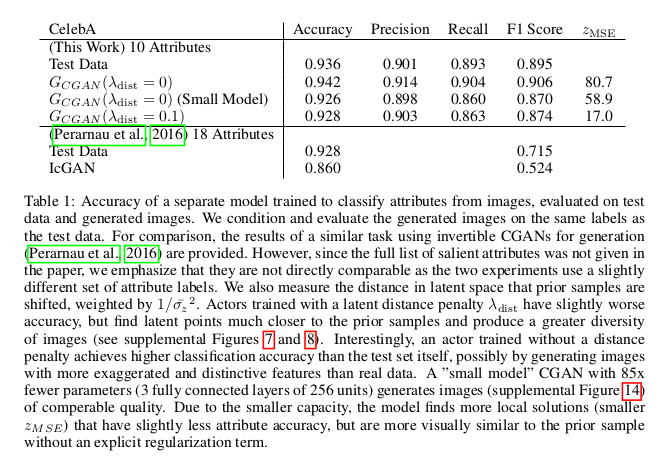
文章还将LSTM VAE做了实验,这里不展开说明,详情可以参看原文。
值得说的是再数据集下加入新的标签数据时,不需要重新训练生成网络,只需要更新一下先验分布$p(z)$和标签数据的后验分布$q(z \vert x)$的映射网络 就可以实现新的标签下的有条件生成,这样将大大降低模型训练的成本,是文章的很大的优势所在。
总结
Latent Constraints通过约束无条件生成模型的潜在空间,展示了一种新的条件生成方法。这种条件生成方法可以大大降低模型在新增标签数据下的训练 成本,有一定的指导意义。同时Latent Constraints也算是将VAE和GAN做了结合,在这一方面也带来了新的启示。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










