Cross Domain Image Generation through Latent Space Exploration with Adversarial Loss论文解读
跨模态之间转换生成在模态间差异大的时候是相对困难的,将一个模态编码得到的潜在变量作为条件在GAN的训练下映射到另一个模态的潜在变量是 Cross Domain Image Generation through Latent Space Exploration with Adversarial Loss 的核心。虽然这篇论文只是预印版,但是文章的这个跨模态潜在变量相互映射的思想是很有启发性的。
论文引入
人类很容易学会将一个领域的知识转移到另一个领域,人类可以灵活地学习将他们已经在不同领域学到的知识连接在一起,这样在一个领域内的条件下, 他们就可以回忆或激活他们从另一个领域学到的知识。深度生成模型通过将它们映射到潜在空间来编码一个域内的隐式知识是被广泛使用的。 可以控制潜在变量通过条件在学习域内生成特定样本。然而,与人类相比,深层生成模型在从一个域到另一个域之间建立新连接方面不够灵活。 换句话说,一旦它学会了从一组域条件生成样本,使其用于生成以另一组控制为条件的样本通常很难并且可能需要重新训练模型。
跨域转换对于建立模态之间的联系是重要的,能够让神经网络更加地智能化,有一些方法提出来解决跨模态的问题。 将条件编码映射到无条件训练的VAE[1],以允许它用用户定义的域有条件地生成样本,并取得了很好的效果。 但是一个限制是那些条件是通过one-hot专门定义的。这样做需要特征工程,并且想要对一些隐含的特征进行条件化时效果较差, 例如使用来自一个场景的图像作为条件来生成学习域中的相关图像。在Unsupervised cross-domain image generation 中训练端到端模型,假设这两个域相关性,再循环训练。
今天要说的这篇论文,为了在更少的模态假设下实现跨模态的相互生成,总结一下这篇论文的优势:
- 利用GAN实现了跨模态的潜在变量之间的相互映射
- 在较少的假设下实现跨模态的转换
实现方法
我们一起来看一下文章实现的模型框架:
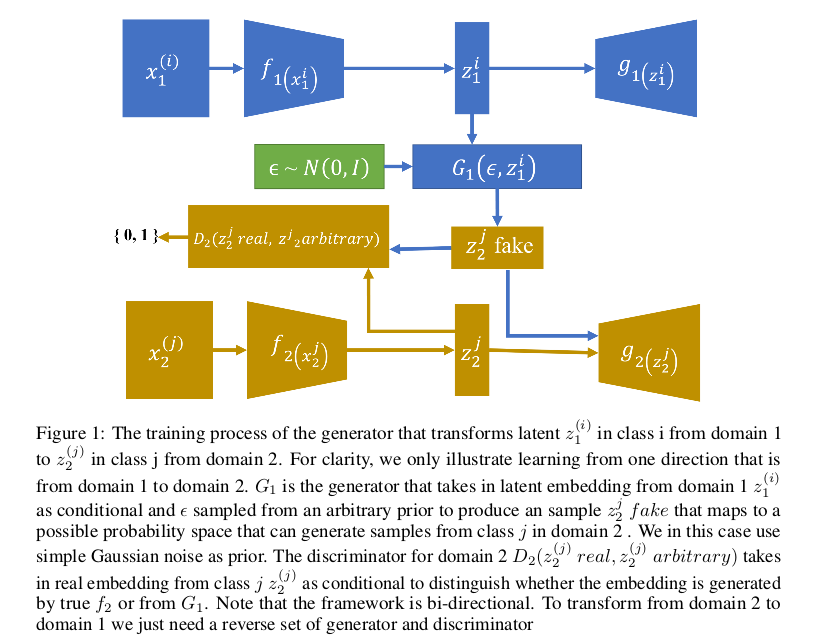
下标为1的代表着是模态1下的数据变换,相对应的下表为2的代表着模态2下的数据变换,上标代表着模态下的类别,$i$类和$j$类。$f$代表着编码器网络, $g$代表着解码器网络,$G$代表了实现映射的生成器,$D$代表了对应的判别器,噪声$\epsilon \sim \mathcal N(0,1)$。
我们看到上下两路对应的是VAE实现框架,也就是上路为模态1对应的$VAE_1$是一个完整的流程,下路为模态2对应的$VAE_2$也是一个完整的流程, 当训练$VAE_1$和$VAE_2$到收敛状态时(训练完成),此时的编码器已经可以很好的将模态数据编码到隐藏空间了,我们分析有模态1到模态2的变换。 模态1的第$i$类图像$x_1^{(i)}$作为输入到模态1的编码器$f_1(x_1^{(i)})$从而得到$i$类的潜在变量$z_1^i$,将$z_1^i$作为条件, $\epsilon$作为噪声输入到生成器$G_1$下从而实现映射到,模态2第$j$类的图像经过编码得到的潜在空间下,此时由生成器$G_1$得到的映射记为$z_2^j fake$。 判别器$D_2$的目的是为了判别真实模态2下$j$类图像编码得到的$z_2^j real$和生成的$z_2^j fake$是否是匹配,如果不匹配就认为是假,如果匹配了 那就说明生成器$G_1$成功欺骗了判别器$D_2$从而实现相互博弈共同提高。相对应的,由模态2也可以向模态1映射,这个过程和模态1到模态2是相似的。
分析了框架的实现方法我们再看一下实现的损失函数上的设计,首先是VAE对应的损失优化,这个大家估计也都熟悉了:
\[ELBO = \max_{\theta} \max_{\phi} E_{p_{D(x)}}[-KL(q_{\phi}(z \vert x),p(z)) + E_{q_{\phi}(z \vert x)}log p_{\theta}(x \vert z)]\]ELBO下参数的定义和原始VAE下是相同的,我就不重复描述了,为了达到更好的VAE结果,文章还加了一个像素上的重构误差,所以最终VAE下的损失函数为:
\[\mathcal L(\theta , \phi, x^{(i)}) = \frac{1}{N} \sum_{i=1}^N [\lambda_1 \mathcal C(x^{(i)},g(f(x^{(i)}))) + \lambda_2 ELBO^{(i)}]\]这里的$\mathcal C$就是像素上的重构误差,${\lambda_1,\lambda_2}$为控制的参数,这个损失将实现VAE的整体优化。对于映射上的GAN的损失函数设计, 文章主要采用匹配的方法博弈,文章匹配有三组。一组是真实匹配$z,z$,对应的损失记为$\mathcal L_{c=1}(z,z) \equiv -log(D(z,z))$; 一组是生成上的匹配$z,z^{\prime}$,其中$z^{\prime}$为生成的隐藏变量,对应的损失记为$\mathcal L_{c=0}(z,z^{\prime}) \equiv -(1 - log(D(z,z^{\prime})))$; 最后一组是噪声对应的匹配$z,\epsilon$,对应的损失记为$\mathcal L_{c=0}(z,\epsilon) \equiv -(1 - log(D(z,\epsilon)))$。 则最终的判别器的损失:
\[\mathcal L_D = \mathbb E_{z \sim p(z \vert x)}[\mathcal L_{c=1}(z,z)] + \mathbb E_{z \sim G(z,\epsilon)}[\mathcal L_{c=0}(z,z^{'})] + \mathbb E_{\epsilon \sim p(\epsilon)}[\mathcal L_{c=0}(z,\epsilon)]\]在生成器中文章引入了正则项$\frac{1}{n} \Vert \epsilon - G(\epsilon ,z) \Vert_2^2$,当生成器将简单噪声移动到映射分布时, 通常会最大化所生成的输出与原始噪声$\epsilon$之间的距离。随着这个术语的增加,最小化损失函数以防$G$和$\epsilon$太远。综合上述, 对于G的损失函数可以写为:
\[\mathcal L_G = \mathbb E_{z \sim p(z), \epsilon \sim p(\epsilon)}[\mathcal L_{c=1}G(z,\epsilon) + \frac{\lambda_{reg}}{n} \Vert \epsilon - G(\epsilon, z) \Vert_2^2]\]经过对上述损失函数优化,系统将达到平衡,此时就可以实现跨模态的相互生成。输入模态1下的$x_1^{(i)}$经过编码得到$z_1^i$,经过GAN的映射得到 $z_2^j fake$送入到模态2的解码器下得到输出$x_2^{(j)^{‘}}$,从而实现了模态间的转换。
实验
文中主要是在MNIST数据集和SVHN数据集下进行的实验,$MNIST \to MNIST$的实现下的模态转换主要是实现${0 \to 5, 1 \to 6, 2 \to 7, 3 \to 8, 4 \to 9}$, 其中${0,1,2,3,4}$为模态1下的数据,${5,6,7,8,9}$为模态2下的数据,得到的生成的实验结果如下:
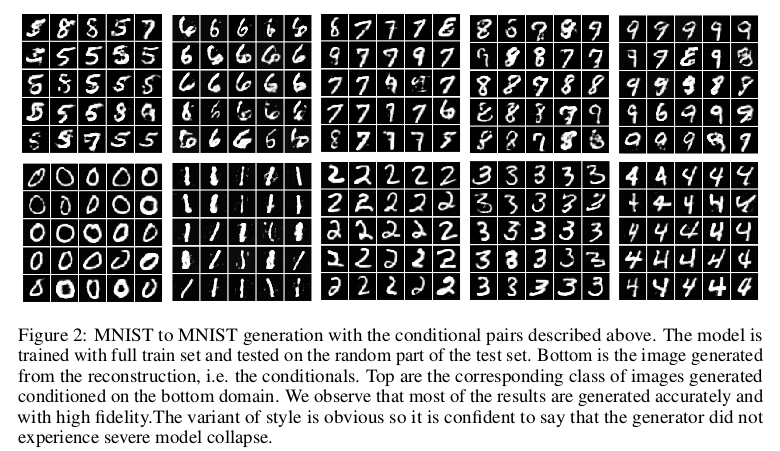
对于SVHN到MNIST的转换,由于SVHN下没有0这个数字,所以转换为${1 \to 6, 2 \to 7, 3 \to 8, 4 \to 9}$,结果如下:

在定量分析上,文中为生成的数据设计了分类器用来检测生成数据的分类效果,侧面反应生成的质量,同时也做了人体辨别实验:
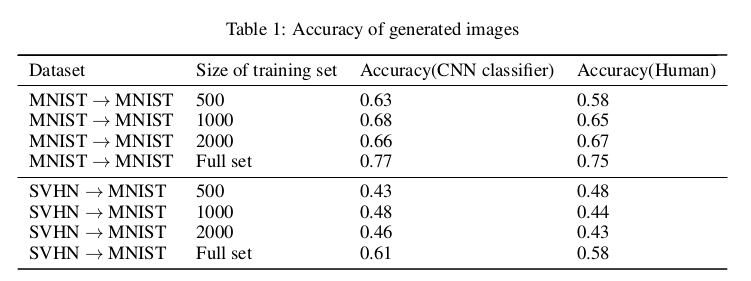
文中还补充了MNIST到Fashion-MNIST转换的实验,实验生成上得到了不错的效果:

由于只是预印版,所以一些详细的对比实验没有加进去,不过这种方法的启发意义还是蛮大的。
总结
文章利用GAN的思想在VAE的基础上,实现了模态间的潜在空间的相互映射,得到映射的空间可以进一步的解码生成对应于另一个模态的数据,从而实现了 跨模态的相互生成。这种利用潜在空间的变换实现跨模态生成在很多跨模态之间都可以参考,虽然文章只是预印版但是很具有启发意义。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










