JMVAE-h JMVAE-kl论文解读
VAE在图像和数据的生成上有着不错的效果,对于单模态数据而言VAE可以不错的重构出图像(虽然有些模糊),但是对于双模态或者是更多模态下的利用VAE 则是困难的,JMVAE可以用于双模态的相互生成但是对于模态间维度差异很大或者是一个模态下缺失数据的情况下效果则是不乐观,这篇论文就是在JMVAE 的基础上为了克服模态下缺失数据造成的生成不理想提出了JMVAE-h和JMVAE-kl两种模型用于改进。
论文引入
虽然图像可以由像素信息表示,但这些也可以用文本或标签信息来描述,双向交换这些信息对于掌握信息是有价值的,我们脑海中想象一副图像通过描述成文字的 形式表达出来,有这段描述如果可以生成出对应的图片就是信息的双向交换。JMVAE-h和JMVAE-kl就是在图像和文本上做双向生成,但是也不限于这两个模态, 接下来的讨论就是在图像和文本双模态的基础上展开的。
图像(实值和密集)和文本(离散和稀疏)具有不同类型的尺寸和结构,因此,模态之间的关系可能具有很高的非线性。实现模态之间双向生成的一种主要 方法是训练在模态特定网络中共享隐藏层顶部的网络体系结构[1]。 这种方法的显着优点是具有多种模态的模型可以端到端地训练,并且训练的模型可以提取联合表示,这是一种集成所有模态的更紧凑的表示。 如果模型可以正确地获得模态间的联合表示,则该模型可以通过该表示从另一模态容易地生成一种模态。另一种简单的方法是为每个模态创建各自的网络并独立地训练它们, 然而,当双向生成模态时,所需网络的数量预计会随着模态的增加而呈指数增长。而且在训练期间每个网络的隐藏层不会同步,因此这种简单的方法在实现双向生成上是不足的。
为了生成不同的模态,将模态间联合表示建模为概率潜在变量是很重要的。这是因为,不同的模态具有不同的结构和维度,因此它们的关系不应该是确定性的。 基于MCMC方法在DBM上训练是可行的,但是对于特别高维的数据就是相当困难的了。
变分自动编码器(VAE),作为深度模型由于可以使用反向传播来训练,所以在高维数据处理上比DBM有很大的优势。因此,可以尝试将VAE扩展到能够双向生成模态的模型。 这种扩展方法思路上很简单,与以前的神经网络和DBM方法一样,共享对应于每种模态的生成模型的潜在变量,称这个模型为联合多模态变分自动编码器(JMVAE)。 但是在高维模态下当缺少想要生成的数据时,JMVAE的潜在变量(即联合表示)会崩溃,并且无法成功生成此模态。
综合以上的原因,这篇论文提出了两个改进模型,JMVAE-kl和JMVAE-h。JMVAE-kl设计了一个新的编码器,除了JMVAE的编码器之外,每种模态都有一个输入, 并减少它们之间的分布差异;JMVAE-h将潜变量分为随机等级结构。
总结一下,这篇论文的优势:
- 提出了两个模型,JMVAE-kl和JMVAE-h,它们可以有效防止潜在变量在缺少高维模态时崩溃
- 模型的双向生成能力与单向VAE类似
- 模型可以适当获得包含不同模态信息的联合表示,可做双向生成
JMVAE、JMVAE-h、JMVAE-kl
我们先对比一下这三个模型的结构:
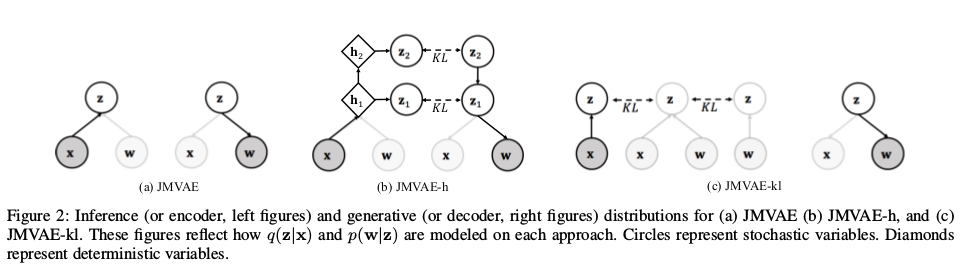
上图中$x$是一个模态,可以认为是图像模态,$w$是另一个模态,可以认为是文本模态。JMVAE直接用联合分布z做中间过渡;JMVAE-h则是采用分层采样到潜变量; JMVAE-h是通过训练两个额外的编码器再通过KL散度将潜变量拉近到联合分布z上。接下来我们分块详细说明各个模型。
JMVAE:
想要理解好一个模型,除了框架上的理解外就是对损失优化的理解,掌握这两块深度学习的基本模型都是可以理解的,VAE的中文资料推荐看一下苏剑林关于 VAE讲解的博客[2],通俗易懂(不愧是数学出身)也可以看我之前的博客[3], 相比之下逊色很多。对于JMVAE在VAE的基础上处理双模态:
\[\mathcal L_{JM}(x,w) = -D_{KL}(q_\phi (z \vert x,w) \Vert p(z)) + E_{q_\phi (z \vert x,w)}[log p_{\theta_x}(x \vert z)] + E_{q_\phi (z \vert x,w)}[log p_{\theta_w}(w\vert z)]\]这里的z就是双模态的联合表示,通过z可以decoder出两种模态的生成,对于由$x,w$编码得到的$q_\phi (z \vert x,w)$通过KL散度将其拉向先验分布$p(z)$ 这里的$p(z)$和VAE中都是标准高斯正态分布$\mathcal N(0,1)$,后面两项是为了优化decoder得到的数据与原始数据的误差。
通过训练JMVAE可以得到两个模态的联合表示,但是在模态数据缺失(不是全部确实,部分数据确实或者数据不充足)的情况下,这种联合表示是脆弱的, 为了改进这个问题,进而有了JMVAE-h和JMVAE-kl。
JMVAE-h:
JMVAE-h是在JMVAE的基础上对潜在变量z对其做分层,使其具有层次结构。假设对因变量分为了L层$z_1,…,z_L$,此时JMVAE的联合表示$p(x,w)$ 可以表示为$p(x,w) = \int … \int p_{\theta}(z_L)p_{\theta}(z_{L-1}\vert z_L)…p_{\theta}(x\vert z_1)p_{\theta}(w\vert z_1)dz_1…dz_L$ 其中所有条件分布$p_{\theta}(z_{l-1}\vert z_l)$都是高斯分布。对于隐变量分布$q_{\phi}(z_1,…,z_L \vert x,w)=q_{phi}(z_1 \vert x,w)…q_{phi}(z_L \vert x,w)$, 其中所有条件分布$q_{phi}(z_l \vert x,w)$都是高斯分布。通俗点说,$x,w$编码得到隐变量$z_1$,$z_1$再通过神经网络做变换(分层)到$z_2$ 这样一直下去直到第L层,文中定义$L=2$。此时的损失函数为:
\[\begin{aligned} \mathcal L_{JM_h}(x,w) = -\sum_{l=1}^L E_{q_\phi (z_{l+1} \vert x,w)}D_{KL}(q_\phi (z_l \vert x,w) \Vert p_{\theta}(z_l \vert z_{l+1})) \\ + E_{q_\phi (z_1 \vert x,w)}[log p_{\theta_x}(x \vert z_1)] + E_{q_\phi (z_1 \vert x,w)}[log p_{\theta_w}(w\vert z_1)] \end{aligned}\]通过对隐变量分层,通过不断迭代可以对数据编码得到的隐空间更好地区分开,从而可以较好的学习到每个模态数据编码后对应的隐变量从而较好的解决了 数据模态确实带来的生成上的崩溃。
JMVAE-kl:
JMVAE-h虽然较好的解决模态缺失问题但是迭代采样是耗时的,尤其是处理高维数据的时候,如果我们已经有了单模态下编码得到的隐变量$q_{\lambda}(z \vert x)$, 另一个模态的隐变量$q_{\lambda}(z \vert w)$,对于联合分布$q_\phi (z \vert x,w)$,将单模态的隐变量和联合分布一一拉近,最后的联合分布将是包含两个模态编码信息的隐变量。 但是由于单独训练了单模态的编码器,所以解码过程出的数据质量相对要好。
对于JMVAE-kl的损失函数:
\[\mathcal L_{JM_kl}(x,w) = \mathcal L_{JM}(x,w) - [D_{KL}(q_\phi (z \vert x,w) \Vert q_{\lambda}(z \vert x)) + D_{KL}(q_\phi (z \vert x,w) \Vert q_{\lambda}(z \vert w))]\]JMVAE-kl需要单独训练编码器,相比代价高一点,但是生成的质量要高一点,后面实验部分也有说明。
模型对比
实验选取的数据集是mnist和celebA,对于JMVAE、JMVAE-h、JMVAE-kl在2维潜变量结果如下:
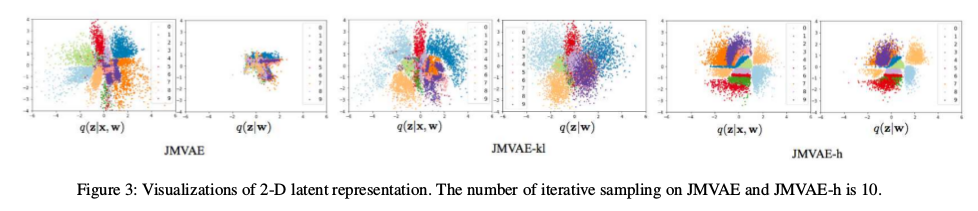
可以看到JMVAE-kl和JMVAE-h在潜变量上更加开,这样说明了潜变量有更好地区分度。在评估方法上,采用对数似然衡量,越小说明模型效果越好:
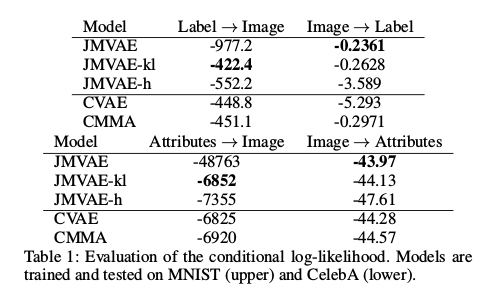
在mnist和celebA上,JMVAE-h和JMVAE-kl都展示出了比JMVAE更好地实验效果:


总结
这篇论文在JMVAE的基础上在改进输入模态缺失的问题上提出了JMVAE-h和JMVAE-kl。但是如果高维数据缺失过于严重的话,也很难对数据做还原, 但是JMVAE-kl和JMVAE-h可以适当地缓解这类问题,能够在数据模态缺失下生成合理的数据,这类扩展是有意义的,而且也具有代表性, 不仅仅可以在图像和文本上处理,同时也可以在更多模态上试验。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










