马尔科夫链应用在很多的领域，对于复杂的分布求解和采样达到了很实际的效果。虽然目前深度学习比较火的任然是深度神经网络的应用， 但是马尔科夫链在深度学习中占据着很重要的地位。Improving Sampling From Generative Autoencoder With Markov Chains 将马尔科夫链应用在了生成自编码器上，改善了潜在空间与先验分布不一致的问题，实现了较高质量的图像生成。

引入

　　目前已发表文章中比较出名的生成自编码器（Generative Autoencoders）有两个，一个是很有名的VAE（之前博客有简单提过，后续准备再详细写一篇关于VAE的博客）， 另一个就是AAE（之前博客有写过）。 两种模型的整体思路都是在Autoencoder的基础上将Encoder得到的潜在空间使其服从先验分布。VAE通过KL缩小潜在向量与标准高斯分布间的距离， 使得潜在向量服从\(N(0,1)\)分布；AAE通过GAN思想的引入，将先验分布视为正样本，Encoder得到的潜在空间视为假样本，通过对抗使得Encoder得到的潜在空间服从先验分布。 但是这样得到的潜在空间一定严格服从先验分布吗？论文中用了may not回答了这个问题！

　　如果可以利用马尔科夫链采样潜在空间，再通过潜在空间和先验分布不断缩小实现潜在空间严格服从先验分布，从而提高生成图像的质量。 这就是论文所要实现的目的。

　　先按照论文的格式来定义一下变量，为了方便描述这里引用VAE的模型框架来描述：

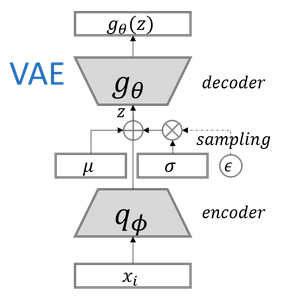
　　对于Encoder和Decoder如果大家对自编码了解的肯定都很熟悉了，Encoder就是将数据样本\(X\)进行编码得到潜在空间\(Z\)，Decoder就是将\(Z\)解码还原成数据样本\(X'\)。 \(Q_\phi (Z\vert X)\)表示条件分布数据样本\(X\)下得到的潜在空间\(Z\)的分布，\(P_\theta (X\vert Z)\)表示条件分布潜在空间\(Z\)下得到的数据样本\(X'\)的分布。 其中的\(\phi\)为Encoder网络参数，\(\theta\)为Decoder的网络参数。Encoder网络可以用\(e(X;\phi)\)表示，Decoder网络可以用\(d(Z;\theta)\)表示。 为了更好的描述VAE和AAE得到的潜在向量不一定严格服从先验分布，我们来看看数学上的解释。

　　按照定义实际网络训练中，\(x_0 \sim P(X)\)其中P(X)为真实数据样本的分布表示\(x_0\)为真实数据样本服从真实数据样本分布，\(z_0 \sim Q_\phi (Z\vert X=x_0)\) 编码得到的潜在向量\(z_0\)服从潜在空间的分布，解码得到的\(x_1\)服从\(x_1 \sim P_\theta (X\vert Z=z_0)\)。通过训练希望潜在向量服从先验分布 \(z_0 \sim P(Z)\), 实际数据样本服从解码器得到的样本分布\(x_0 \sim P_\theta (X\vert Z=z_0)\)。

　　如果满足上述表述，由全概率的定义有\(\int Q_\phi (Z\vert X) P(x) dX = P(Z)\)，这个等式成立的前提是潜在空间严格服从先验分布， 如果定义潜在空间服从分布\(\hat{P}(Z)\)，满足上式需\(P(Z) = \hat{P}(Z)\)，但是在训练初期由于潜在空间和先验分布并没有很相近这个等式很难成立，所以上式应写为：

\[\int Q_\phi (Z\vert X) P(X) dX = \hat{P}(Z)\]

　　同样的道理，对于解码得到的分布全概率表示应由\(\int P_\theta (X\vert Z) P(Z) dZ = P(X)\)换为:

\[\int P_\theta (X\vert Z) \hat{P}(Z) dZ = P(X)\]

　　通过不断的优化潜在空间分布\(\hat{P}(Z)\)和先验分布\(P(Z)\)间的差距来实现\(P(Z) = \hat{P}(Z)\)，这就是MCMC采样的优点所在， 避免了一定程度上由于训练导致解码生成的图片的不真实（文中使用unrealistic artifacts描述）。论文中指出MCMC采样可将任何潜在空间移动到可能的学习潜在分布区域， 意思就是MCMC可以很好的实现潜在空间向先验分布的靠拢，并且避免产生不真实的图片。下图是实验的一部分，我们先来分析一下：

　　图中a与c图是原始的VAE实现面部变化的过程图，我们可以看到中间过度区域出现了一定的重影部分，而b与d为MCMC采样后VAE的实现， 可以看出重影这样的不真实图像确实是改进了。

　　论文中的另外一大贡献就是在去噪VAE上的效果，论文指出利用MCMC采样得到采样去处理去噪可以减小视觉伪影，并且可以揭示降噪标准的影响。

　　总结一下MCMC采样应用到生成自编码器的优点：

  • 能够更好更加合理的将潜在空间分布向先验分布拉近；
  • 在去噪生成自编码器上能够实现更好的效果，并且可以解释降噪标准对实验的影响。

方法实现及证明

方法实现

　　MCMC采样应用到生成自编码器上，可以用下图更好地理解：

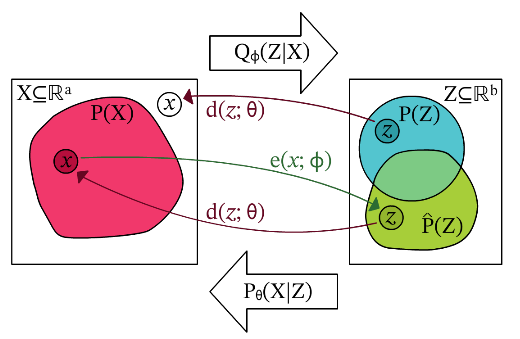
　　从图中可以看到\(P(Z)\)与\(\hat{P}(Z)\)并不是完全一致的，在训练阶段中采样\(\hat{P}(Z)\)然后经过Decoder重构数据样本， 通过优化潜在空间分布和先验分布差异来实现潜在空间逐渐向先验分布靠拢，重构的损失可以是mse损失，交叉熵损失来优化重构和原始样本的差异。

　　对于实现潜在空间逐渐向先验分布靠拢的损失是根据模型框架决定，如果是VAE模型就是利用KL来拉拢两者。即\(L_{prior} = D_{KL}[Q_\phi (Z\vert X)\lvert P(Z)]\) 进一步计算后就是\(L_{prior} = \frac{1}{2} \sum_{n=1}^{N} \mu^2 + \sigma^2 - log(\sigma^2) - 1\)，这就是VAE实现的方法。 对于AAE则是采用GAN的思想通过对抗让潜在空间分布与先验分布相近，损失函数与标准GAN相近，就不在赘述。

　　至于MCMC采样应用于去噪生成自编码器上就是在VAE的基础上在样本上加入噪声的操作，加入的噪声\(\tilde{x} \sim C(\tilde{X} \vert X)\)， 其他的操作和VAE做重构的思路是一样的，包括损失函数的设计也是一样的。

证明

　　马尔科夫链定义如下：

\[T(Z_{t+1} \vert Z_t) = \int Q_\phi (Z_{t+1} \vert X) P_\theta (X\vert Z_t)dX\]

　　其中，\(x_{t+1} \sim P_\theta (X\vert Z_t), z_{t+1} \sim Q_\phi (Z \vert X_{t+1})\)

当\(t \geq 0\)，根据转移算子\(T(Z_{t+1} \vert Z_t)\)绘制样本产生马尔可夫链。

　　接下来，我们把论文中的证明简单说一下，不具体展开。

定理1.如果\(T(Z_{t+1} \vert Z_t)\)定义了一个遍历马尔可夫链\({Z_1,Z_2,...,Z_t}\)，那么链将从任意初始分布收敛到平稳分布\(\pi (Z)\)。 平稳分布\(\pi (Z) = \hat{P}(Z)\)。

　　这个定理的详细证明在另一篇论文中。

引理1.\(T(Z_{t+1} \vert Z_t)\)定义了一个遍历马尔可夫链。

　　这个引理的证明的思路就是从马尔科夫链的满足条件出发，主要从分布都是大于0出发，具体证明就不展开，在本论文的附录中有详细的证明。

引理2.由\(T(Z_{t+1} \vert Z_t)\)定义的链的平稳分布是\(\pi (Z) = \hat{P}(Z)\)。

　　有了上述的说明，最终想表达的是马尔科夫链\(T(Z_{t+1} \vert Z_t)\)是合理的且平稳分布就是\(\hat{P}(Z)\)。

　　对于去噪的情况，上述证明依旧成立，只是马尔科夫链变为：

\[T(Z_{t+1} \vert Z_t) = \int Q_\phi (Z_{t+1} \vert \tilde{X}) C(\tilde{X} \vert X) P_\theta (X\vert Z_t)dX\]

实验

　　论文在实验上没有具体展开，主要是在两个数据集上实现。一个是celebA另一个是svhn数据集，我们看看实验结果：

　　从实验结果上可以看得出来，MCMC采样对于VAE和AAE生成的结果上确实视觉上有所提高。

总结

　　MCMC采样应用在生成自编码器上改善了Encoder编码得到的潜在空间向先验分布靠拢的过程，同时提高了生成图像的质量，在去噪图像还原上的效果改善。 通过图像间差值生成过程可以看出生成的图像更加的合理。MCMC采样将马尔科夫链应用在Autoencoder上提高了整体性能，可以看出采样的方法适用于深层网络的改善， 具有一定的启发意义。

谢谢观看，希望对您有所帮助，欢迎指正错误，欢迎一起讨论！！！