马尔可夫链蒙特卡罗方法简析
对于复杂的分布,要想对其采样如果采取取随机数去拟合后验分布的话,难度特别大。马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC) 方法帮我们解决了这个问题,整体的思路就是利用平稳分布去代替复杂的分布再去取样拟合最终得到复杂样本的分布。所以MCMC方法是个十分有意义的方法, 我们今天来看看具体实现的思路。
知识回顾
在正式说MCMC方法实现之前,我们要先来回顾一下马尔科夫链的一系列知识。
马氏链定理: 如果一个非周期马氏链具有转移概率矩阵\(P\),且它的任何两个状态是连通的,那么\(\displaystyle \lim_{n\rightarrow\infty}P_{ij}^n\) 存在且与\(i\)无关,记\(\displaystyle \lim_{n\rightarrow\infty}P_{ij}^n = \pi(j)\),此时:
\[\displaystyle \lim_{n \rightarrow \infty} P^n =\begin{bmatrix} \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}\]有
\[\displaystyle \pi(j) = \sum_{i=0}^{\infty}\pi(i)P_{ij}\]\(\pi\)是方程\(\pi P = \pi\)的唯一非负解
其中
\[\pi = [\pi(1), \pi(2), \cdots, \pi(j),\cdots ], \quad \sum_{i=0}^{\infty} \pi_i = 1\]\(\pi\)称为马氏链的平稳分布。
细致平稳条件: 如果非周期马氏链的转移矩阵\(P\)和分布\(\pi(x)\)满足
\[\begin{equation} \pi(i)P_{ij} = \pi(j)P_{ji} \quad\quad \text{for all} \quad i,j \end{equation}\]则\(\pi(x)\)是马氏链的平稳分布,上式被称为细致平稳条件(detailed balance condition)。其实这个定理是显而易见的, 因为细致平稳条件的物理含义就是对于任何两个状态\(i,j\), 从\(i\)转移出去到\(j\)而丢失的概率质量,恰好会被从\(j\)转移回\(i\)的概率质量补充回来, 所以状态\(i\)上的概率质量\(\pi(i)\)是稳定的,从而\(\pi(x)\)是马氏链的平稳分布。数学上的证明也很简单,由细致平稳条件可得
\[\begin{align*} & \sum_{i=1}^\infty \pi(i)P_{ij} = \sum_{i=1}^\infty \pi(j)P_{ji} = \sum_{i=1}^\infty \pi(j)P_{ji} = \pi(j) \\ & \Rightarrow \pi P = \pi \end{align*}\]由于\(\pi\)是方程\(\pi P = \pi\)的解,所以\(\pi\)是平稳分布。
MCMC算法-Metropolis-Hastings采样
假设我们已经有一个转移矩阵为\(Q\)马氏链(\(q(i,j)\)表示从状态\(i\)转移到状态\(j\)的概率,也可以写为\(q(j|i)\)或者\(q(i\rightarrow j)\), 显然,通常情况下\(p(i) q(i,j) \neq p(j) q(j,i)\)也就是细致平稳条件不成立,所以\(p(x)\)不太可能是这个马氏链的平稳分布。我们可否对马氏链做一个改造, 使得细致平稳条件成立呢?比如,我们引入一个\(\alpha(i,j)\), 我们希望
\[\begin{equation} \label{choose-alpha} p(i) q(i,j)\alpha(i,j) = p(j) q(j,i)\alpha(j,i) \quad (*) \end{equation}\]取什么样的\(\alpha(i,j)\)以上等式能成立呢?最简单的,按照对称性,我们可以取
\[\alpha(i,j)= p(j) q(j,i) 和 \quad \alpha(j,i) = p(i) q(i,j)\]于是\((*)\)式就成立了。所以有
\[\begin{equation} \label{detailed-balance} p(i) \underbrace{q(i,j)\alpha(i,j)}_{Q'(i,j)} = p(j) \underbrace{q(j,i)\alpha(j,i)}_{Q'(j,i)} \quad (**) \end{equation}\]于是我们把原来具有转移矩阵\(Q\)的一个很普通的马氏链,改造为了具有转移矩阵\(Q'\)的马氏链,而\(Q′\)恰好满足细致平稳条件, 由此马氏链\(Q′\)的平稳分布就是\(p(x)\)!
在改造\(Q\)的过程中引入的\(\alpha(i,j)\)称为接受率,物理意义可以理解为在原来的马氏链上,从状态\(i\)以\(q(i,j)\)的概率转跳转到状态 \(j\)的时候,我们以\(\alpha(i,j)\)的概率接受这个转移,于是得到新的马氏链\(Q′\)的转移概率为\(q(i,j)\alpha(i,j)\)。
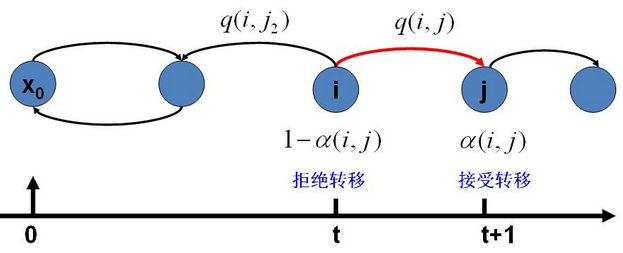
假设我们已经有一个转移矩阵\(Q\)(对应元素为\(q(i,j)\)), 把以上的过程整理一下,我们就得到了如下的用于采样概率分布\(p(x)\)的算法。

上述过程中\(p(x),q(x\vert y) 说的都是离散的情形,事实上即便这两个分布是连续的,以上算法仍然是有效,于是就得到更一般的连续概率分布\)p(x)\(的采样算法,而\)q(x\vert y)$$就是任意一个连续二元概率分布对应的条件分布。
以上的 MCMC 采样算法已经能很漂亮的工作了,不过它有一个小的问题:马氏链Q在转移的过程中的接受率\(\alpha(i,j)\)可能偏小, 这样采样过程中马氏链容易原地踏步,拒绝大量的跳转,这使得马氏链遍历所有的状态空间要花费太长的时间,收敛到平稳分布\(p(x)\)的速度太慢。 有没有办法提升一些接受率呢?
假设\(\alpha(i,j)=0.1, \alpha(j,i)=0.2\),此时满足细致平稳条件,于是
\[p(i)q(i,j)\times 0.1 = p(j)q(j,i) \times 0.2\]上式两边扩大5倍,我们改写为
\[p(i)q(i,j) \times 0.5 = p(j)q(j,i) \times 1\]我们提高了接受率,而细致平稳条件并没有打破!这启发我们可以把细致平稳条件\((**)\)式中的\(\alpha(i,j),\alpha(j,i)\)同比例放大, 使得两数中最大的一个放大到1,这样我们就提高了采样中的跳转接受率。所以我们可以取
\[\alpha(i,j) = \min\left\{\frac{p(j)q(j,i)}{p(i)q(i,j)},1\right\}\]于是,经过对上述MCMC 采样算法中接受率的微小改造,便得到了Metropolis-Hastings 算法。

MCMC算法-Gibbs采样
对于高维的情形,由于接受率\(\alpha\)的存在(通常\(\alpha <1\)), 以上 Metropolis-Hastings 算法的效率不够高。 能否找到一个转移矩阵\(Q\)使得接受率\(\alpha=1\)呢?我们先看看二维的情形,假设有一个概率分布\(p(x,y)\),考察\(x\)坐标相同的两个点 \(A(x_1,y_1),B(x_1,y_2)\),可得
\[\begin{align*} p(x_1,y_1)p(y_2|x_1) = p(x_1)p(y_1|x_1)p(y_2|x_1) \\ p(x_1,y_2)p(y_1|x_1) = p(x_1)p(y_2|x_1)p(y_1|x_1) \end{align*}\]所以得到
\[\begin{equation} \label{gibbs-detailed-balance} p(x_1,y_1)p(y_2\vert x_1) = p(x_1,y_2)p(y_1\vert x_1) \quad (***) \end{equation}\]即
\[p(A)p(y_2\vert x_1) = p(B)p(y_1\vert x_1)\]基于以上等式,我们发现,在\(x=x_1\)这条平行于\(y\)轴的直线上,如果使用条件分布\(p(y\vert x1)\)做为任何两个点之间的转移概率, 那么任何两个点之间的转移满足细致平稳条件。同样的,如果我们在\(y=y_1\)这条直线上任意取两个点\(A(x_1,y_1),C(x_2,y_1)\),也有如下等式 \(p(A)p(x_2|y_1) = p(C)p(x_1|y_1)\)。
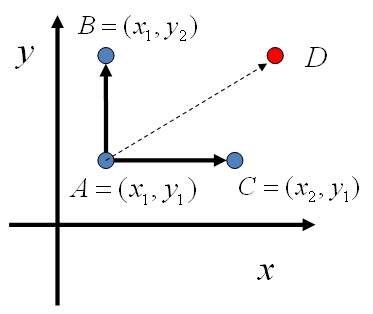
于是我们可以如下构造平面上任意两点之间的转移概率矩阵\(Q\)
\[\begin{align*} Q(A\rightarrow B) & = p(y_B|x_1) & \text{如果} \quad x_A=x_B=x_1 & \\ Q(A\rightarrow C) & = p(x_C|y_1) & \text{如果} \quad y_A=y_C=y_1 & \\ Q(A\rightarrow D) & = 0 & \text{其它} & \end{align*}\]有了如上的转移矩阵\(Q\), 我们很容易验证对平面上任意两点\(X,Y\), 满足细致平稳条件
\[p(X)Q(X\rightarrow Y) = p(Y) Q(Y\rightarrow X)\]于是这个二维空间上的马氏链将收敛到平稳分布\(p(x,y)\)。而这个算法就称为 Gibbs Sampling 算法,是 Stuart Geman 和Donald Geman 这两兄弟于1984年提出来的,之所以叫做Gibbs Sampling 是因为他们研究了Gibbs random field, 这个算法在现代贝叶斯分析中占据重要位置。

以上采样过程中,如图所示,马氏链的转移只是轮换的沿着坐标轴\(x\)轴和\(y\)轴做转移,于是得到样本 \((x_0,y_0), (x_0,y_1), (x_1,y_1), (x_1,y_2),(x_2,y_2), \cdots\)马氏链收敛后,最终得到的样本就是\(p(x,y)\)的样本, 而收敛之前的阶段称为 burn-in period。
上述的二维Gibbs采样可以拓展到\(n\)维。
总结
在贝叶斯公式得到的后验分布将变得非常复杂时,马尔科夫链蒙特卡罗方法帮助解决了此类问题。Metropolis-Hastings采样和Gibbs采样是MCMC的两大算法, 围绕着贝叶斯和此类采样问题整体的思路基本上就是这些。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










