前段时间一直在讨论朴素贝叶斯和贝叶斯思想，当然前面博文中的贝叶斯的应用只是冰山一角，还有很多贝叶斯的发展没有说，我们以后有机会会慢慢的更新。 今天我们一起来看看贝叶斯思想在生成对抗网络(GAN)中的应用。BayesianGAN将数据生成的半监督学习做到了很好的水平，很值得我们去学习一下。

引入

　　高维自然信号的概率分布学习是一个很大的挑战因为这些隐性的数据分布很难用显性似然建模，但是近年来随着GAN的诞生和发展让不可显性表示的数据可以较好的被学习到。 然而GAN存在着一些固有的问题，训练过程不好把握、模式崩溃(mode collapse)导致的生成结果多样性不足、生成结果扭曲等问题。尽力刻画数据分布的GAN来说输出可解释的多种候选样本是很重要的。 来自 Uber AI Lab 的 Yunus Saatchi 等人，提出了利用一个简单的贝叶斯公式进行端到端无监督/半监督 GAN 学习。最值得说的是论文在半监督学习上的效果还是很显著的。

　　深度学习对大量标签数据的依赖是显而易见的，这也成为抑制深度学习发展的一个潜在要素之一。长久以来，科学家们都在探索使用尽量少的标签数据， 希望实现从监督式学习到半监督式学习再到最后的无监督式学习的转化。较少的利用标签去学习建模数据样本是重要的发展方向也是难点， BayesianGAN在GAN的框架下使用了动态的梯度哈密尔顿蒙特卡罗（Hamiltonian Monte Carlo）边缘化这些后验来将生成网络和判别网络中的权重最大化。 其获得结果的方法非常的直接，并且在不需要任何标准的干预，比如特征匹配或者mini-batch discrimination的情况下，都获得了良好的表现。

　　GAN的训练是基于最小-最大优化的，通常会对后验机制在整个网络的权重进行衡量，把其作为一个单一节点上的一个聚焦点。这样一来，即便生成器不对训练样本进行存储， 也希望生成器中的样本与数据分布中得到的样本是完全相关的。利用生成器与判别器中的参数后验数据分布，是贝叶斯思想的思考方式，合理的利用后验分布能实现更好地对数据样本表示。 BayesianGAN便将这一理论实现了，论文的推理是直接进行的、可解释的、稳定的。在实验上整个框架都不需要参数匹配，正则化或者任何的特别（ad-hoc）技巧。

　　BayesianGAN利用生成器参数的多峰后验，在生成器不同的参数设置下可以生成不同风格的图片，我们先把论文中实验结果展示一下：

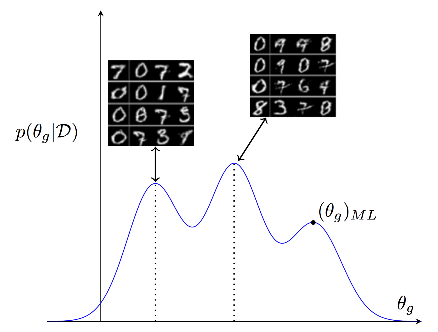
　　我们总结了BayesianGAN的优势所在：

• 在半监督学习问题上的准确预测；
• 对优秀性能的最小干预；
• 响应对抗反馈的推断的概率公式；
• 避免模式崩溃；
• 展示多个互补的生成和判别模型，形成一个概率集成（probabilistic ensemble）。

BayesianGAN模型介绍

　　BayesianGAN的网络结构和传统GAN是相同的，都是仅有生成器判别器组成。为了更加形象的说明，我们贴上一张传统GAN的网络结构。

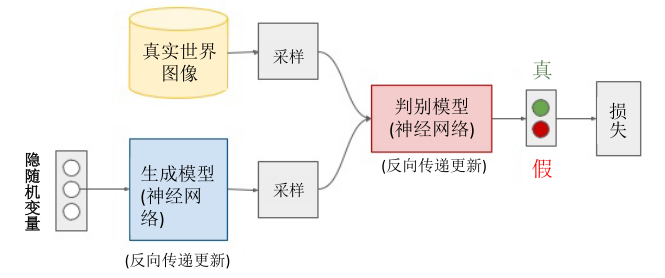
　　BayesianGAN的创新之处就在于利用生成器与判别器的网络参数去后验生成数据样本概率从而实现生成样本分布与实际数据样本分布最大化相似。 \(G(z;\theta _g )\)表示生成器在随机先验分布（多为白噪声）z（\(z \sim p(z)\)）传入下生成假样本，生成器作用过程受其网络参数\(\theta _g\)控制。 判别器\(D(x;\theta _d )\)表示对真假样本判断，作用过程受网络参数\(\theta _d\)控制。

无监督学习

　　如何后验\(\theta _g,\theta _d\)便是文章的重点所在，论文从条件后验迭代采样来解决的：

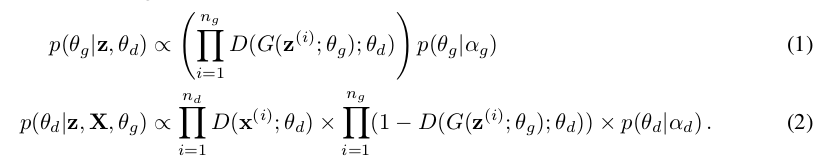
　　其中，\(p(\theta _g \vert \alpha _g)\)和\(p(\theta _d \vert \alpha _d)\)分别是超参数\(\alpha _g\)和\(\alpha _d\)对应为生成器和判别器的先验值。 \(n _g\)与\(n _d\)对应是生成器和判别器的小批量样本数量，相对应的定义样本。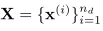

　　通过前几篇博客对贝叶斯原理的梳理，我从大体上想理解上面的式子应该不算困难。对于公式1我们可以看到通过先验概率\(p(\theta _g \vert \alpha _g)\) 与条件\(n _g\)参数在判别器网络迭代相乘可以表示\(n _g\)参数在判别器作用下的后验概率，同理可解释判别器参数。

　　如果上述描述不是很清晰的话，我们从整体上理解这个式子。判别器对于生成数据的判断理想情况下应该为0，但是在优化生成器时，生成器的目的是尽可能的让判别器D误判， 也就是希望\(D(G(z^{(i)};\theta _g);\theta _d)\)为1，当然这是理想状态，所以每一次迭代更新将根据生成器参数\(\theta _g\) 先验概率和判别器传来的条件概率来修正生成器的参数。同样的判别器在生成器参数和已有真实数据的作用下，是尽可能区分真假数据，从而更新内部参数。

　　所以，参数的相互更新促使了生成器与判别器之间的博弈，达到同步提高的作用，上面的式子可以进一步变化为：

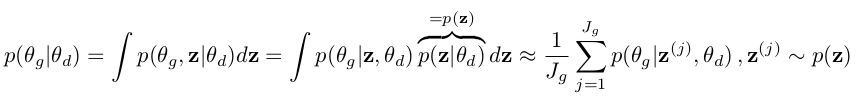
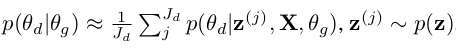
　　有了这个公式，就可以在程序中实现参数的更新了，具体的可以参考论文的论代码。

半监督学习

　　半监督学习是BayesianGAN的很大的突破，对于标签定义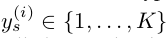为，标签为0时对应的判别为生成样本， 标签非零时认为数据为真实的，对应于无监督学习，此时的参数后验概率为：

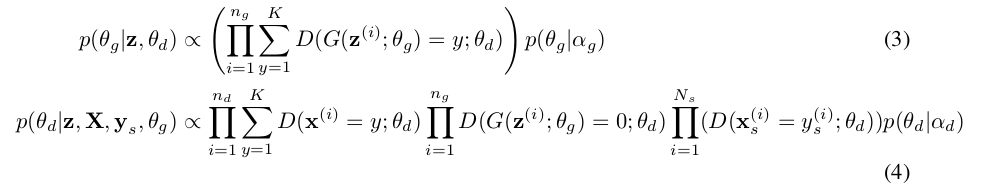
　　\(n _g\)表示来自生成器的小批量样本，\(n _d\)为无标签的样本，\(N_s\)为标签样本。从上式，我们可以得到， 在式3中生成器为了欺骗判别器尽可能更新参数使得判别器判断其标签为非0，对应的判别器尽可能将生成样本标签判为0。由于此为半监督学习，其中， \(N_s \ll n\)。在后续的实验中我们可以知道，标签数据仅仅占据总样本的0.2%。

　　上面公式也可以做以下近似变换：

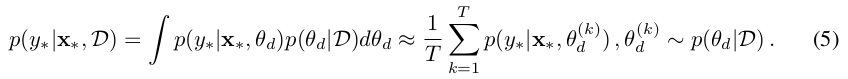
模型实现

　　对于模型的具体实现，我们可以看看文中给出的伪代码：

　　整体更新的过程就是最大化后验分布，从而实现生成器与判别器之间的对抗。对于梯度优化的选择，文中强调使用SGHMC，使用的原因如下：

• SGHMC与动量SGD关系密切，SGD在GAN训练上的经验丰富;
• 从SGD可以直接导入参数设置（如学习率和动量）到SGHMC;
• 贝叶斯方法对GAN推断的许多实际益处来自探索对SGHMC启用的生成器的权重\(\theta _g\)的丰富的多模式分布。

BayesianGAN实验

　　BayesianGAN实验上注重对GAN的多样性不足问题的解决说明。

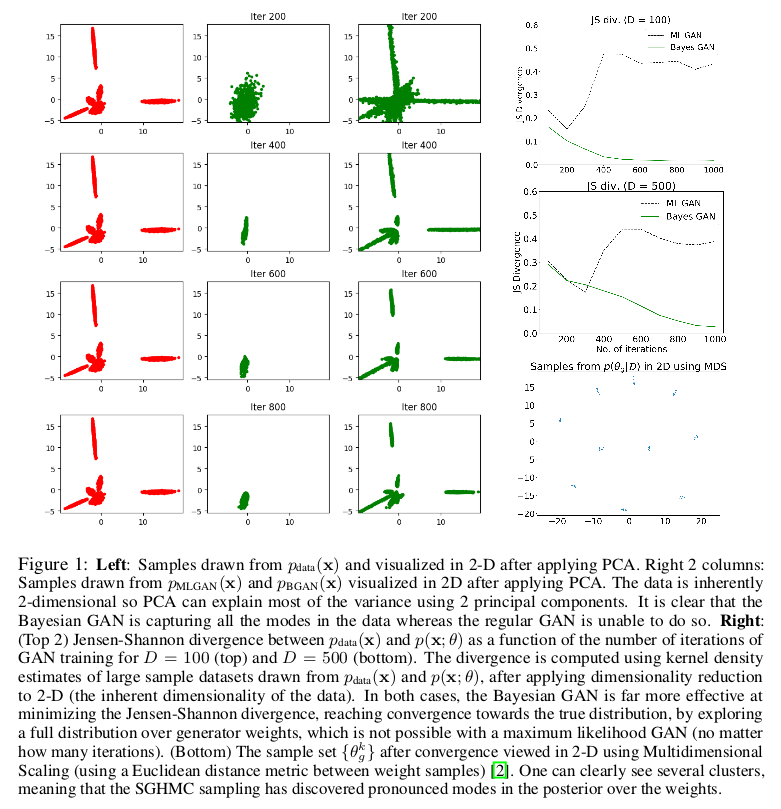
BayesianGAN在数据分类上的效果是显著的：

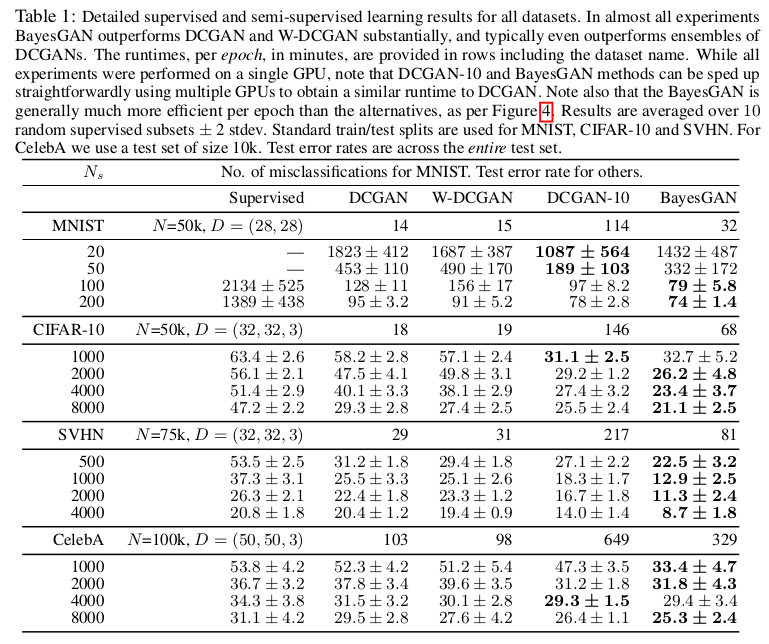
BayesianGAN通过更改生成器的权重，可以实现生成效果的多风格：

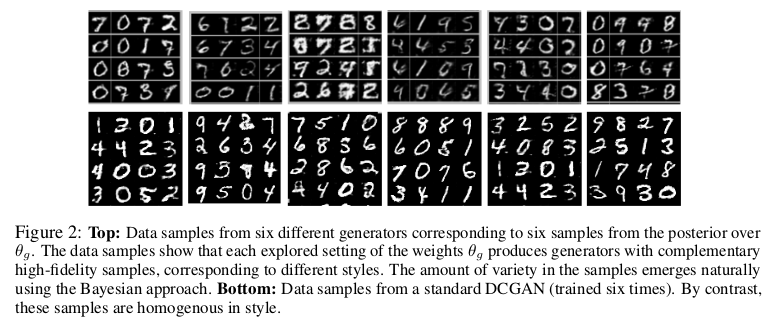
总结

　　BayesianGAN作者提出了一个简单的贝叶斯公式，用于GAN中的端到端的无监督和半监督学习。在这个框架内， 使用动态的梯度Hamiltonian Monte Carlo将生成器和判别器的权重posteriors进行边际化。作者对从生成器中获得的数据样本进行了分析， 在生成器的权重中，展示了跨越几个独特模型的探索。还展示了在学习真正的分布的过程中，数据和循环的有效性。

　　BayesianGAN的tensorflow版本代码已经公布，具体地址在这里。

　　由于论文中涉及的理论高度较高，如果文中有任何错误的地方，欢迎指正！

谢谢观看，希望对您有所帮助，欢迎指正错误，欢迎一起讨论！！！