入门跨模态我们需要什么基础
跨模态检索,跨模态生成是近年来较为火热的研究方向,随着计算机计算能力的大大提高以及深度神经网络的普遍应用对于跨模态的发展是正向推动的。 今天我们来整理一下入门跨模态我们需要知道些什么?
什么是跨模态检索
模态是指数据的存在形式,比如文本、音频、图像、视频等文件格式。有些数据的存在形式不同,但都是描述同一事物或事件的。而我们在信息检索的需求往往不只是同一事件单一模态的数据, 也可能需要其他模态的数据来丰富我们对同一事物或事件的认知,此时就需要跨模态检索来实现不同模态数据之间的检索。不同模态之间的数据差别是很大的, 比如给你一张比基尼美女的图片,再配以对比基尼美女的文字描述,再来一张比基尼美女的素描,甚至再来一段声音。这些模态之间想建立联系是较为复杂的, 如何实现跨模态的相互认识,我们需要把这些模态整理一下,简单的说就是让它们尽量一致。很多的方法是将数据映射到子空间分析。
什么是子空间学习(Subspace learning methods)
子空间学习大意是指通过投影,实现高维特征向低维空间的映射,是一种经典的降维思想。例如人脸图像,如果每幅图像提取出来的特征是1000维,则每幅图像对应着1000维空间中的一个点。 维数太高给计算带来很多问题,且很多人认为真实有效的人脸图像特征并没有那么高维,可能只有100维,即每幅人脸只是100维空间中的一个点。将特征从1000维压缩到100维, 就是子空间学习问题。在模式识别中,可能绝大多数的维数约简(降维,投影)算法都算是子空间学习,如PCA, LDA, LPP, LLE等等。子空间学习的主要问题, 就是如何将特征从高维空间压缩到低维空间,需要保留什么样的信息,设定什么样的准则,低维空间的特征具有哪些特征等问题。在对数据进行子空间学习之前,我们要对数据做前期处理。
前期数据处理:中心化,标准化
中心化:将原始数据减去平均数。数据中心化可以让数据更加的整齐,增加基向量的正交性。
标准化:将原始数据减去平均数然后再除以标准差,得到的数据范围是0~1。标准化目的是消除不同变量间量纲差异,自身变异,数值大小带来的影响。
主成分分析(PCA)与典型相关分析(CCA)的异同点
二者在对特征空间降维,映射至子特征空间的计算方法相同,但其对应的解释不同,二者均是通过构造原变量的适当线性组合提取不同信息,主成分分析着眼于考虑变量的“分散性”信息, 而典型相关分析则立足于识别和量化二组变量的统计相关性,是两个随机变量之间的相关性在两组变量之下的推广。我的之前博客有对PCA的详细描述, 详情请看这里。CCA我倒是没有写个这类博客,我们简单了解下CCA。
CCA的计算思想
典型相关分析CCA最朴素的思想:首先分别在每组变量中找出第一对典型变量,使其具有最大相关性,然后在每组变量中找出第二对典型变量,使其分别与本组内的第一对典型变量不相关, 第二对本身具有次大的相关性。如此下去,直到进行到R步,两组变量的相关性被提取完为止,可以得到R组变量。
以上的基本思想可以完成各模态间的子空间的学习,这是入门跨模态最为基础的一步,再复杂的今天我们也不去说,接下来说说对于一般实验效果的评判标准和方法。
机器学习性能评估指标
混淆矩阵
True Positive(真正, TP):将正类预测为正类数.
True Negative(真负,TN):将负类预测为负类数.
False Positive(假正, FP):将负类预测为正类数 误报(Type I error).
False Negative(假负,FN):将正类预测为负类数 漏报(Type II error).

精确率(precision)定义为:
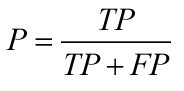
需要注意的是精确率(precision)和准确率(accuracy)是不一样的
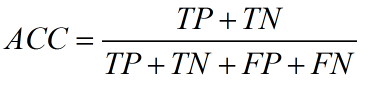
在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量是很少的,一般只有千分之几,如果用acc, 即使全部预测成负类(不点击)acc 也有 99% 以上,没有意义。
召回率(recall,sensitivity,true positive rate)定义为:
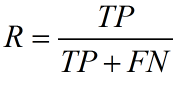
通俗理解精确率和召回率
精确率是针对预测结果而言的,它表示的是预测为正的样本中有多少是对的。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP)。
而召回率是针对原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)。
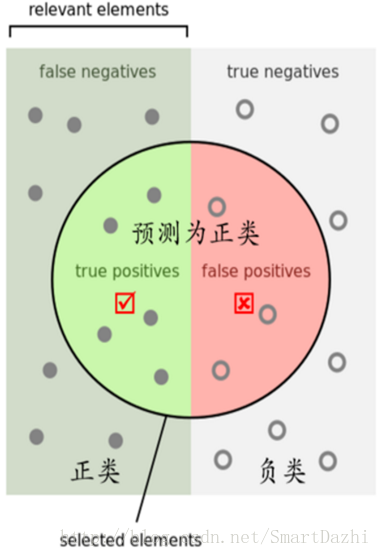

在信息检索领域,精确率和召回率又被称为查准率和查全率


平均正确率(Average Precision, AP):对不同召回率点上的正确率进行平均。
(1)未插值的AP: 某个查询Q共有6个相关结果,某系统排序返回了5篇相关文档,其位置分别是第1,第2,第5,第10,第20位,则AP=(1/1+2/2+3/5+4/10+5/20+0)/6
(2)插值的AP:在召回率分别为0,0.1,0.2,…,1.0的十一个点上的正确率求平均,等价于11点平均
(3)只对返回的相关文档进行计算的AP, AP=(1/1+2/2+3/5+4/10+5/20)/5,倾向那些快速返回结果的系统,没有考虑召回率。
不考虑召回率情况下,单个查询评价指标还有:
Precision@N:在第N个位置上的正确率,对于搜索引擎,考虑到大部分作者 只关注前 一、两页的结果,P@10, P@20对大规模搜索引擎非常有效。
Mean Average Precision(MAP)
即对所有查询的平均正确率(Average Precision, AP)求宏平均。具体而言,单个主题的平均准确率是每篇相关文档检索出后的准确率的平均值。 主集合的平均准确率(MAP)是每个主题的平均准确率的平均值。MAP 是反映系统在全部相关文档上性能的单值指标。系统检索出来的相关文档越靠前(rank 越高), MAP就可能越高。如果系统没有返回相关文档,则准确率默认为0。
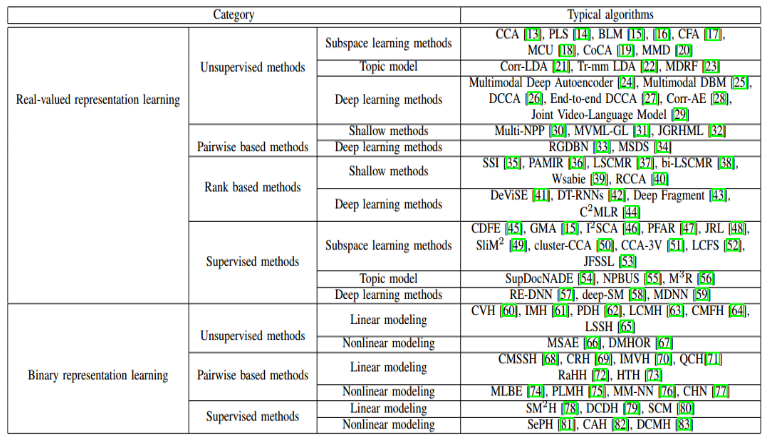
相关研究论文合集
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










