逻辑回归算法在预测和判别应用上很广泛，今天我们一起来看看逻辑回归算法。

1.什么是逻辑回归

逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验 证我们这个求解的模型的好坏。

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）

回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率

2.逻辑回归的优缺点

优点：

1）速度快，适合二分类问题

2）简单易于理解，直接看到各个特征的权重

3）能容易地更新模型吸收新的数据

缺点：

对数据和场景的适应能力有局限性，不如决策树算法适应性那么强

3.逻辑回归和多重线性回归的区别

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两 种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

如果是连续的，就是多重线性回归

如果是二项分布，就是Logistic回归

如果是Poisson分布，就是Poisson回归

如果是负二项分布，就是负二项回归

4.逻辑回归用途

寻找危险因素：寻找某一疾病的危险因素等；

预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；

判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是 属于某病。

5.Regression 常规步骤

寻找h函数（即预测函数）

构造J函数（损失函数）

想办法使得J函数最小并求得回归参数（θ）

6.构造预测函数h(x)

1) Logistic函数（或称为Sigmoid函数），函数形式为：

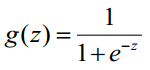
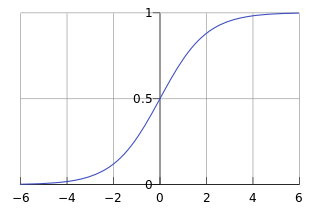
对于线性边界的情况，边界形式如下：

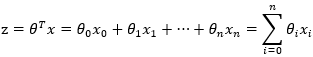
其中，训练数据为向量

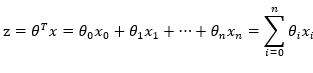
最佳参数

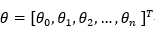
构造预测函数为：

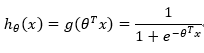
函数h(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

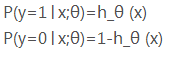
7.构造损失函数J（m个样本，每个样本具有n个特征）

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

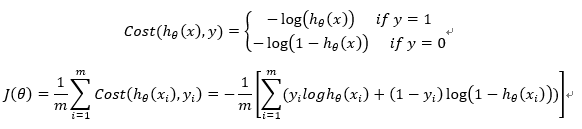
谢谢观看，希望对您有所帮助，欢迎指正错误，欢迎一起讨论！！！