SVM（Support Vector Machines）是分类算法中应用广泛、效果不错的一类。本文将SVM可分类为三类：线性可分（linear SVM in linearly separable case）的线性SVM、线性不可分的线性SVM、非线性（nonlinear）SVM。

今天是2月14号，也是外国的情人节，这个日子对于我们这些单身狗还是比较折磨。今天看到了之前同学有的成对了，心情还是比较复杂的！ 有时候生活就是这么的无奈，好了不说了，我们来看看今天的博文，一起看看SVM算法，SVM在数据分类上的效果还是很不错的，即使在现在 涌出大量的算法中依然占据着一定的江山。

这篇文章只是浅析SVM具体的还请参考其他资料。

1.线性可分：

对于二类分类问题，训练集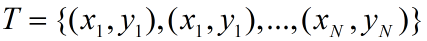，其类别yi∈{0,1}，线性SVM通过学习得到 分离超平面（hyperplane）:

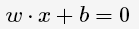
以及相应的分类决策函数：

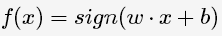
有如下图所示的分离超平面，哪一个超平面的分类效果更好呢？

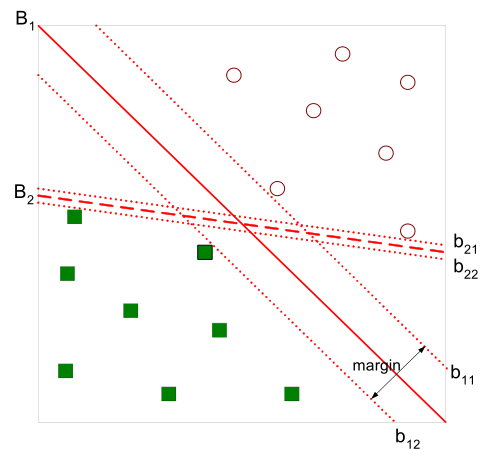
直观上，超平面B1的分类效果更好一些。将距离分离超平面最近的两个不同类别的样本点称为支持向量（support vector）的，构成了 两条平行于分离超平面的长带，二者之间的距离称之为margin。显然，margin更大，则分类正确的确信度更高（与超平面的距离表示分类 的确信度，距离越远则分类正确的确信度越高）。通过计算容易得到：

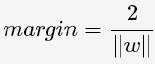
从上图中可观察到：margin以外的样本点对于确定分离超平面没有贡献，换句话说，SVM是有很重要的训练样本（支持向量）所确定的。 至此，SVM分类问题可描述为在全部分类正确的情况下，最大化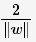（等价于最小化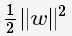）； 线性分类的约束最优化问题：

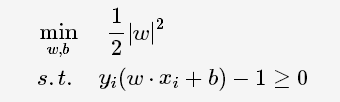
对每一个不等式约束引进拉格朗日乘子（Lagrange multiplier）αi≥0,i=1,2,⋯,N；构造拉格朗日函数（Lagrange function）：

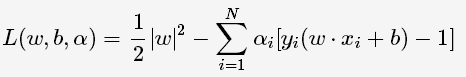
根据拉格朗日对偶性，原始的约束最优化问题可等价于极大极小的对偶问题：

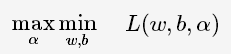
将L(w,b,α)对w,b求偏导并令其等于0，则

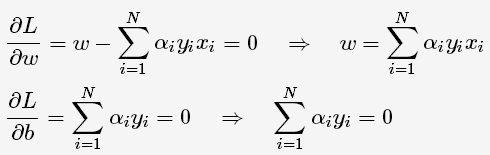
将上述式子代入拉格朗日函数中，对偶问题转为

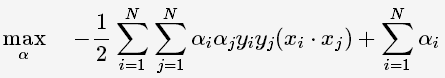
等价于最优化问题：

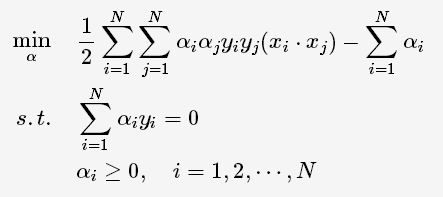
线性可分是理想情形，大多数情况下，由于噪声或特异点等各种原因，训练样本是线性不可分的。因此，需要更一般化的学习算法。

2.线性不可分

线性不可分意味着有样本点不满足约束条件，为了解决这个问题，对每个样本引入一个松弛变量ξi≥0，这样约束条件变为：

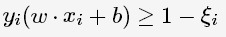
目标函数则变为

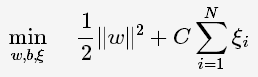
其中，C为惩罚函数，目标函数有两层含义：

1）margin尽量大

2）误分类的样本点计量少

C为调节二者的参数。通过构造拉格朗日函数并求解偏导（具体推导略去），可得到等价的对偶问题：

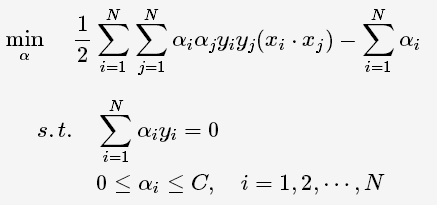
与上一节中线性可分的对偶问题相比，只是约束条件αi发生变化，问题求解思路与之类似。

3.非线性

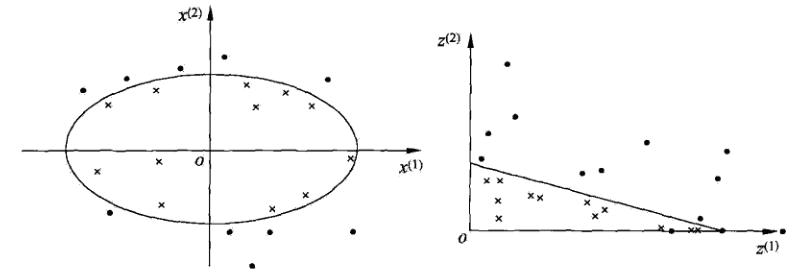
对于非线性问题，线性SVM不再适用了，需要非线性SVM来解决了。解决非线性分类问题的思路，通过空间变换ϕ（一般是低维空间映射 高维空间x→ϕ(x)）后实现线性可分，在下图所示的例子中，通过空间变换，将左图中的椭圆分离面变换成了右图中直线。

在SVM的等价对偶问题中的目标函数中有样本点的内积xi⋅xj，在空间变换后则是ϕ(xi)⋅ϕ(xj)，由于维数增加导致内积计算成本增加，这时 核函数（kernel function）便派上用场了，将映射后的高维空间内积转换成低维空间的函数：

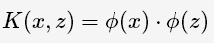
将其代入一般化的SVM学习算法的目标函数中，可得非线性SVM的最优化问题：

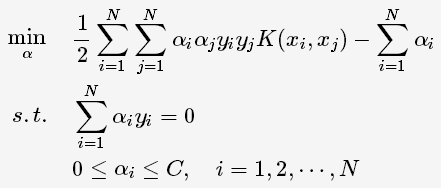
如果有需要了解SVM的详细推导过程，请看下面我的附录中给的笔记

以下是附录部分，请选择性参看。

附录

谢谢观看，希望对您有所帮助，欢迎指正错误，欢迎一起讨论！！！