决策树是一个预测模型，它代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。

我们先一起看一个例子

假设，我们有以下数据，表示当天是否回去玩高尔夫：

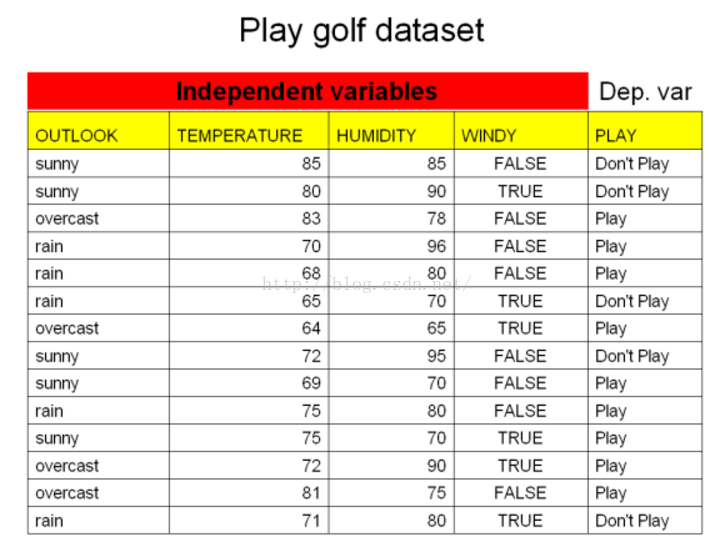
用决策树建立起来后，能得到这样的模型：

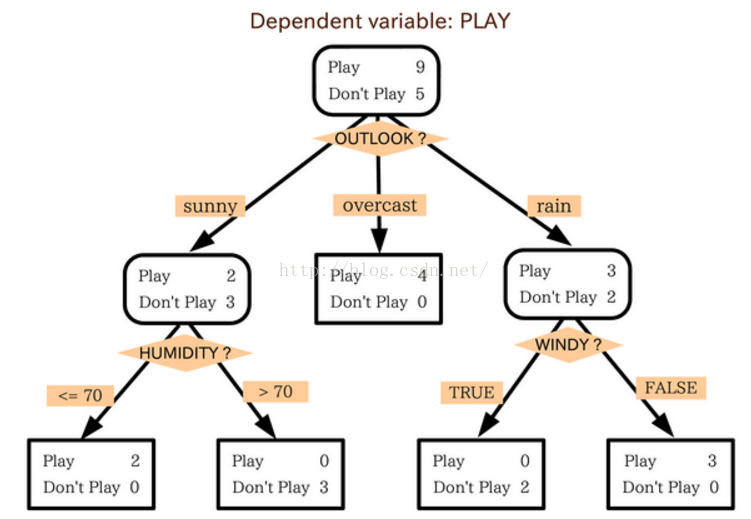
至此可以看出，说白了，决策树就是If()语句的层层嵌套，知道最后能总结出点什么。

决策树中的元素：

决策树中的元素基本和树中的差不多。

最上面的一个称为根节点，如上图的Outlook，用数据中的属性作为根节点或是节点，如Humidity，Windy等。

分支使用的是节点属性中的离散型数据，如果数据是连续型的，也需要转化成离散型数据才能在决策树中展示，如上图将Outlook属性作为根节点，sunny，overcast，rain作为该节点的三个分支。

信息熵 Entropy：

现在，问题来了，在算法中如何确定使用数据的哪个属性作为根节点或是节点。当然不能随便选，我们追求的一直都是最优解，即使是局部最优。因此我们需要引入信息熵这个概念。

1948年，香农提出了“信息熵”概念。一条信息的信息量大小和它的不确定性有直接的关系。我们对一样东西越是一无所知，想要了解它就需要越多的信息。

举个栗子，如果我随机一个1-8之间的数字，给你猜，只回答你是或否。那最好的猜测方式应该是，“是不是在1-4之间？”，如果得到否，我们就知道在5-8之间，如果得到是，我们继续猜“是否在1-2之间？”。这样的话，我们只需要猜3次就能知道这个数到底是几。转化为信息熵公式就是：

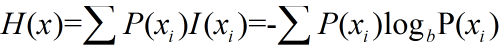
根据这公式和例子，我们能得到结果是3，这是因为我们对1-8数字可能被选取的概率一无所知，如果比如说1-8选取概率并不是均匀分布的，我们就能更快的找到相应的数字，因此信息熵也会相应的变小。

总结下，如果一个变量的不确定越大，熵值也越大。

决策树归纳算法 ID3：

Information Gain：

又称信息获取量或是信息增益，将样本的所有属性分割开，分别计算，熵之和，信息增益就是二者的差值。

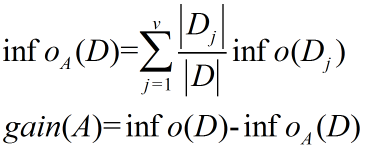
简单理解就是，没有属性A时候的信息量-有A时候的信息量。

举个例子，假设我们有以下数据，买电脑的人与不买电脑的人：

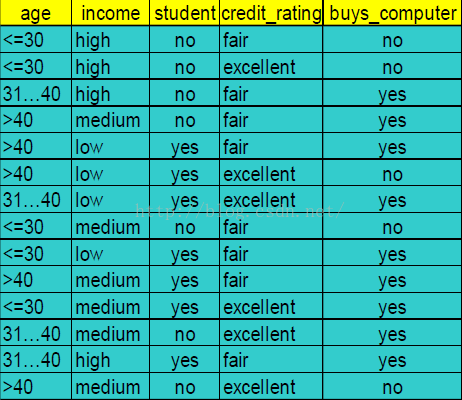
可以看出，在此数据中，总数据量14个，买电脑的人9个，不买电脑的人5个，因此，Info(D)计算方式如下：

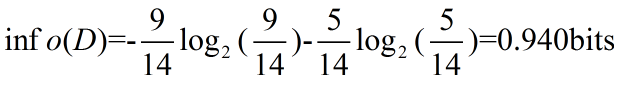
然后，我们想计算下age属性的信息量，<30的5人，<30并买电脑的2人，不买的3人，其余31-40，>40方法同理，因此计算方式如下：

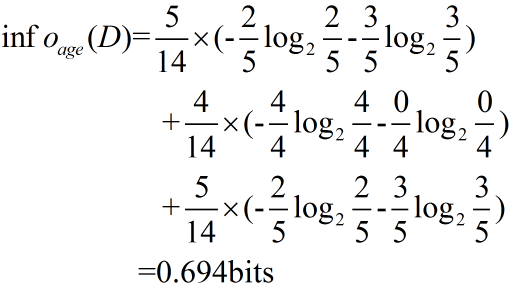
因此Gain(age) = 0.940-0.694 = 0.246

再对比下其余属性Gain(Income)=0.029,Gain(Student)=0.151,Gain(Credit_rating)=0.048，因此可以看出，age属性信息量最大，因此选择age属性作为根节点。计算节点方法同理。

C4.5算法:

ID3算法存在一个问题，就是偏向于多值属性，例如，如果存在唯一标识属性ID，则ID3会选择它作为分裂属性，这样虽然使得划分充分纯净，但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率（gain ratio）的信息增益扩充，试图克服这个偏倚。

C4.5算法首先定义了“分裂信息”，其定义可以表示成：

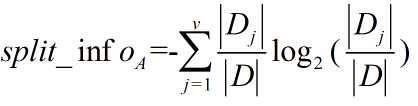
其中各符号意义与ID3算法相同，然后，增益率被定义为：

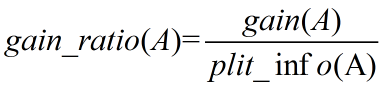
C4.5选择具有最大增益率的属性，ID3选择最大信息获取量的属性，其余没啥差别，也就不赘述了

决策树其余算法：

决策树其余算法还有C4.5，CART算法，共同点为都是贪心算法，区别为度量方式不同，就比如ID3使用了信息获取量作为度量方式，而C4.5 使用最大增益率。

如果属性用完了怎么办：

如果属性全部用完，但是数据还不是纯净集怎么办，即集合内的元素不属于同一类别。就比如上述买电脑的例子中，如果age，Credit_rating， Student，Income都相等，但是有人买电脑，有人不买电脑，那决策树怎么决策？在这种情况下，由于没有更多信息可以使用了，一般对这些子集进行“多数表决”，即使用此子集中出现次数最多的类别作为此节点类别，然后将此节点作为叶子节点。