“距离”、“相似度”汇总
在计算机人工智能领域,距离(distance)、相似度(similarity)是经常出现的基本概念,它们在自然语言处理、计算机视觉等子领域有 重要的应用,而这些概念又大多源于数学领域的度量(metric)、测度(measure)等概念。今天我们一起来汇总一下。
| 英文名 | 中文名 | 公式 | 说明 |
|---|---|---|---|
| Euclidean Distance | 欧式距离 | 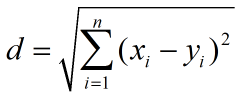 |
以古希腊数学家欧几里得命名的距离;也就是我们直观的两点之间直线最短的直线距离 |
| Manhattan Distance | 曼哈顿距离 | 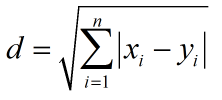 |
是由十九世纪的赫尔曼·闵可夫斯基所创词汇;是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和;也就是和象棋中的“車”一样横平竖直的走过的距离;曼哈顿距离是超凸度量 |
| Minkowski Distance | 闵氏距离 | 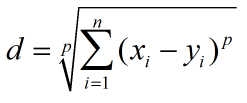 |
以俄罗斯数学家闵可夫斯基命名的距离;是欧式距离的推广,p=2时等价于欧氏距离,和p-范数等值 |
| Hamming Distance | 海明距离 | 逐个字符(或逐位)对比,统计不一样的位数的个数总和 | 所得值越小,参与对比的两个元素约相似;下面是从wikipedia借的4bit的海明距离示意图 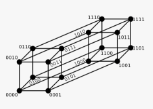 |
| Jaccard Coefficient | 杰卡德距离 | 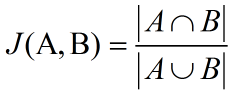 |
越大越相似;分子是A和B的交集大小,分母是A和B的并集大小 |
| Ochiai Coefficient | 未知 | 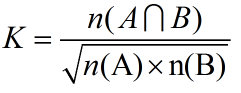 |
|
| Pearson Correlation | 皮尔森相关系数 | 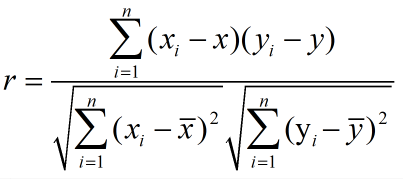 |
分子是两个集合的交集大小,分母是两个集合大小的几何平均值。是余弦相似性的一种形式 |
| Cosine Similarity | 余弦相似度 | 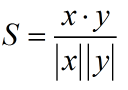 |
|
| Mahalanobis Distance | 马氏距离 | 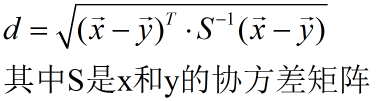 |
印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法;若协方差矩阵是对角阵(diagonal),则该距离退化为欧式距离 |
| Kullback-Leibler Divergence | K-L散度 | 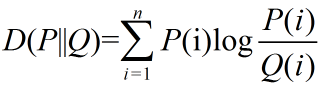 |
即相对熵;是衡量两个分布(P、Q)之间的距离;越小越相似 |
| PMI(Pointwise Mutual Information) | 点对互信息 | 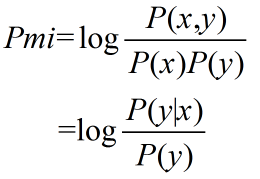 |
利用co-occurance来衡量x和y的相似度;越大越相关;可以看做局部点的互信息(mutual information) |
| NGD(Normalized Google Distance) | 未知 | 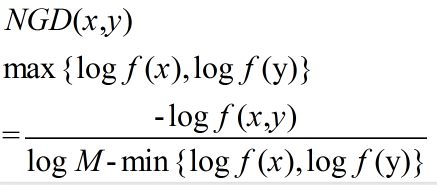 |
这是google用来衡量两个不同的关键字(keyword)的检索结果之间的相关程度;其中f(x)代表包含了关键字x的页面数量,f(x,y)代表同时包含了关键字x和关键字y的页面的数量,M代表google所搜索的总页数;若两个关键字总是成对出现在页面上,那么NGD值为0,相反的,如果两个关键字在所有页面上都没有同时出现过,那么NGD值为无穷;该量是从normalized compression distance (Cilibrasi & Vitanyi 2003)衍生而来的 |
| Levenshtein Distance(Edit Distance) | Levenshtein距离(编辑距离) | 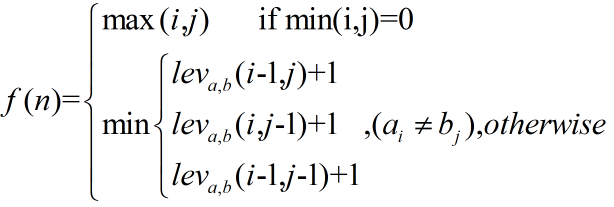 |
是指两个字串之间,由一个转成另一个所需的最少编辑操作次数;俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念;编辑距离越小的两个字符串越相似,当编辑距离为0时,两字符串相等 |
| Jaro-Winkler Distance | 未知 | 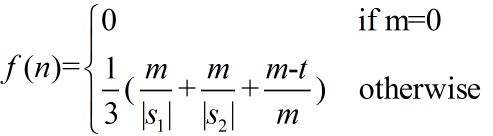 |
|
| Lee Distance | 李氏距离 | 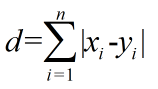 |
在编码理论(coding theory)中两个字符串间距离的一种度量方法 |
| Hellinger Distance | 未知 | 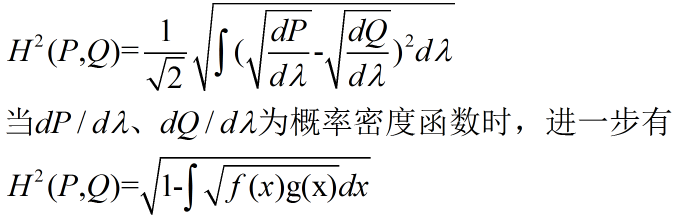 |
注意在作为概率意义的计算时需在测度空间进行;通常被用来度量两个概率分布的相似度,它是f散度的一种;由Ernst Helligner在1909年引进 |
| Canberra Distance | 坎贝拉距离 | 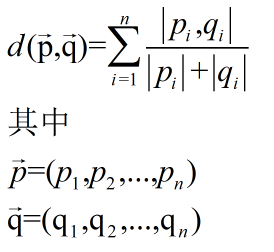 |
|
| Chebyshev Distance | 切比雪夫距离 | 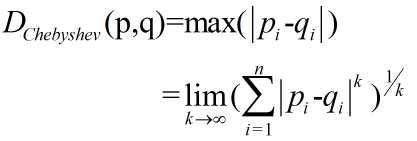 |
切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量,也是超凸度量 |










