激活函数对于数据的制约和变换，线性非线性的函数应用对于神经网络的数据都有很大的意义，今天我们一起来看看激活函数。

激活函数的选择

激活函数是作用于线性函数之后的非线性函数，使得模型具有非线性区分能力。常见的激活函数如下图：

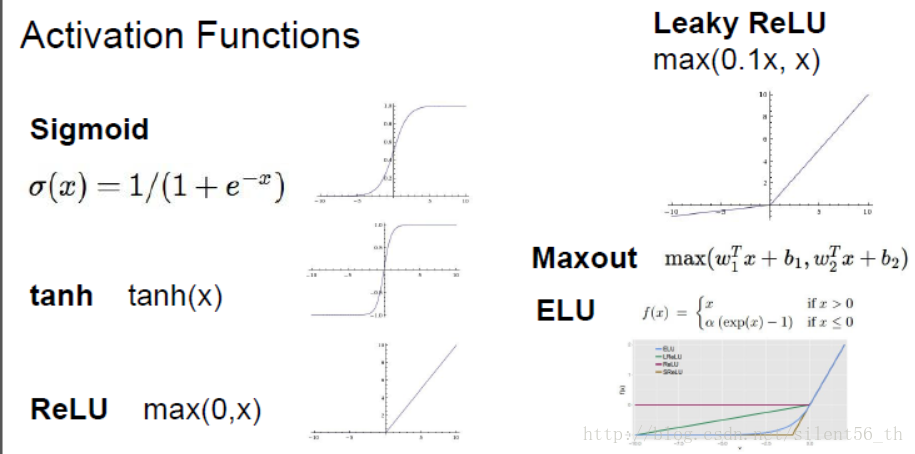
衡量激活函数通常有三个方向的考量：是否会有效地传播gradient；是否是均值为0；计算消耗是否很大。

1. 传播gradient的部分的考量是为了让模型可以快速有效地收敛。

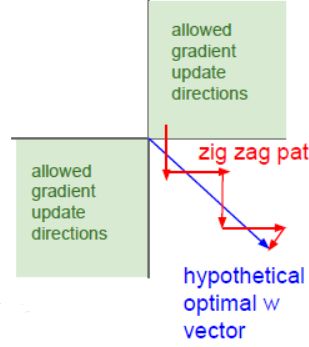
2. 数据集均值为0同样是处于收敛的考虑，举了个特例，然后说有相关论文证明均值为0有助于收敛。如下 图所示，假设所有的输入都大于0，那么考虑从激活函数传回线性函数中的权重的gradient，必然只能位于一三象限（如果是二维的话）， 那么如果理想的方向位于第二象限的话，则需要之字形前行，收敛变慢。

1.sigmoid函数

曾经很火的激活函数，易求导，可解释。但是有很多缺点：对于y接近1以及0的部分，导数几乎为0，所以BP的时候基本不会传播gradient； 不是zero mean的，指数函数计算代价高。

2.tanh 函数

此函数被yann lecun于1991年提出，认为比sigmoid要好。从上诉衡量标准可以看出，tanh具有所有sigmoid的优势以及缺点，除了其是 zero mean的。所以是在这种评价体系中明显优于sigmoid。

3.ReLU函数

函数非常简单，如下图所示，基本就是对于小于0的部分截断，但是具有很多优良的性质，是现在神经网络的默认激活函数，最开始出现 于[Krizhevsky et al., 2012]。

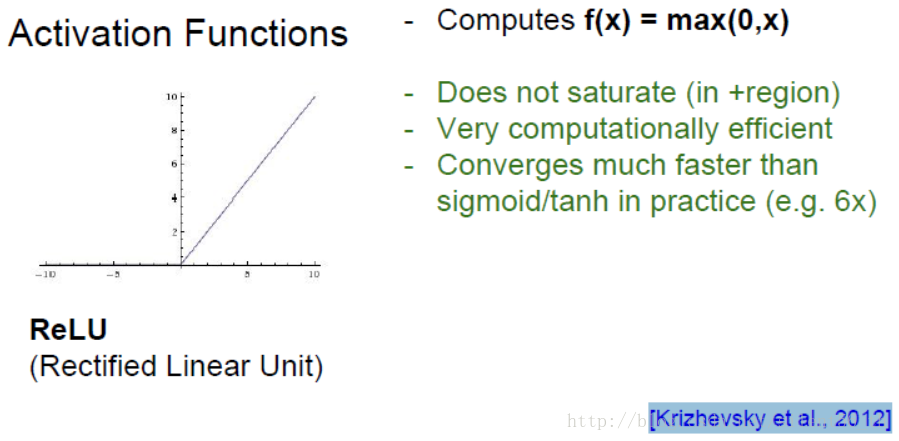
其在大于0的部分直接传回gradient；计算代价很小；实际中收敛速度很快。但是均值不是0；0的部分无法计算梯度；对于小于0的部分 直接kill gradient。如果初始化或者训练过程中，某次的权重恰好使得输出都为0，即无法传回gradient，那么此次优化就会停止在非最 优点无法收敛，如下图所示。

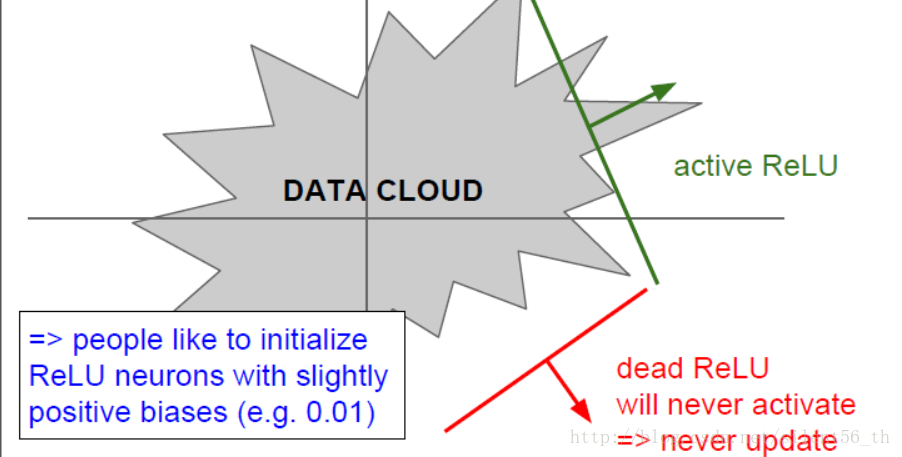
4.ReLU的变种

如上所述，ReLU具有令人难以拒绝的优良性质，但有一些缺点；所以有一些变种用于保留优点，同时修补一些缺点（不收敛）。 Leaky ReLU、Parametric ReLU以及如下图所示：

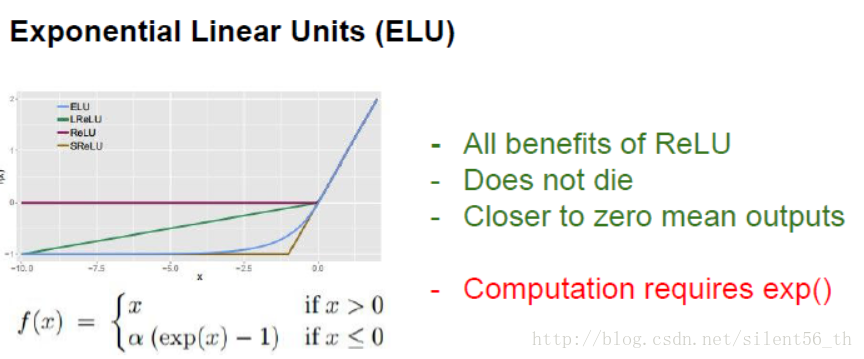
Leaky ReLU用于简单修补ReLU不会收敛的缺点，对于小于0的部分，传回0.01*gradient。而Parametric ReLU则是用于修补Leaky ReLU中 简单实用0.01倍数的缺点，用一个参数替代，注意这个参数不是超参数，是需要在BP中修正的。

ELU则进一步修正ReLU中非zero mean的缺点，它可以证明的预期输出zero mean的数据，但是因为使用了指数函数，计算代价比ReLU要高。

还有一个maxout neuron如下图所示，也是属于ReLU的变种，但变化较大，非线性能力也很强，但是对于整个模型来说参数加倍，并不是 很常用。

5.实际使用的建议

在实际的编程过程中，我使用过sigmoid，tanh，relu，lrelu激活函数，具体的使用技巧可能只有在实验的过程中才有自己的感悟吧。 一般GAN的判别器Discriminator的最后一层往往使用的是sigmoid作为激活，因为要将判别的结果转换为[0,1]间的真假输出。在中间层呢 对于生成器我们经常使用relu激活函数，在判别器的中间层往往使用lrelu激活函数。当然也根据实际GAN模型改变激活函数的使用，具体的 只有大家实际中使用方可知晓。建议使用relu，哈哈！

谢谢观看，希望对您有所帮助，欢迎指正错误，欢迎一起讨论！！！