数据预处理&权重矩阵初始化
数据预处理对于数据的训练和测试都存在很大的意义,如何处理数据是个基础的操作,今天我们一起来看看。
一、数据预处理
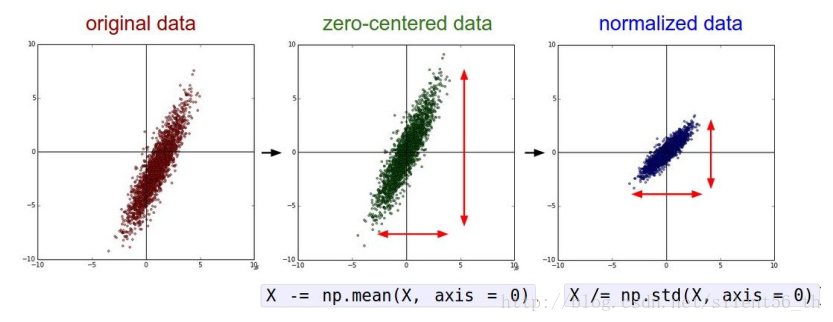
归一化
如下图所示,归一化即使得重心位于原点,方差为1。
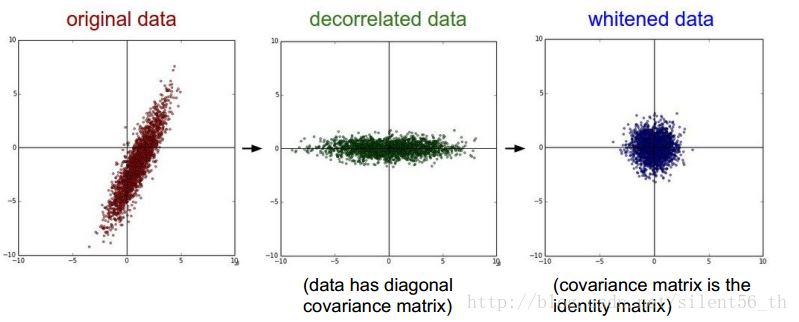
PCA & 白化
如下图所示,PCA是作用于原数据上的一个线性变换,使得协方差矩阵对角化,如果不进行降维的话是不损失信息的。白化进一步使得协 方差矩阵为单位阵。
图像领域中的预处理
由于图像领域的特殊性(例如各维之间不是没有关系的变量,而是具有特定的拓扑结构,所以PCA&白化等涉及旋转变化的部分,会损失这 部分内容,不适用),通常只对图像做zero-centered。而这部分有两种方式:对于每个像素的每个通道求均值,即HxWxC(例如32x32x3) 个均值;还有一种是对于每个通道求均值,即C(例如3)个均值。
二、权值矩阵初始化
都初始化为0
没有gradient传播,因为隐层节点之后的所有数值均为0。非常不可取,永远不要用。
小随机数值
例如:服从均值为0,标准差为1e-2的高斯分布。 对于小型网络适用,但不适合大型深度神经网络。
例如,在十层神经网络的情况下,每层都有500个神经元,适用tanh激活函数,使用上诉小随机数初始化参数得到的各层神经元的分布如下图:
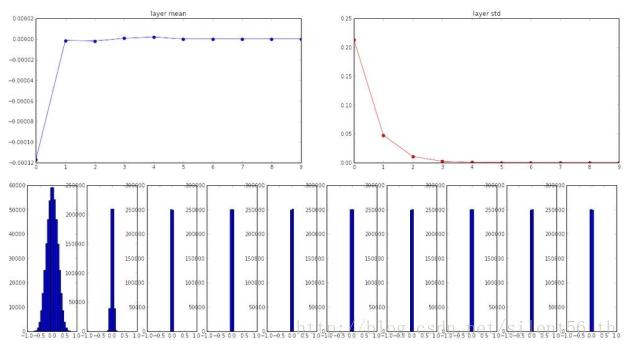
如图到第三层之后的所有神经元的方差都几乎为0,即所有值都可以看做0,同样的gradient不会传播,权值矩阵几乎不会变。
另一个极端是大随机数,例如如果用标准差为1的高斯分布初始化参数,同样的网络设置得到各层神经元的分布如下图:
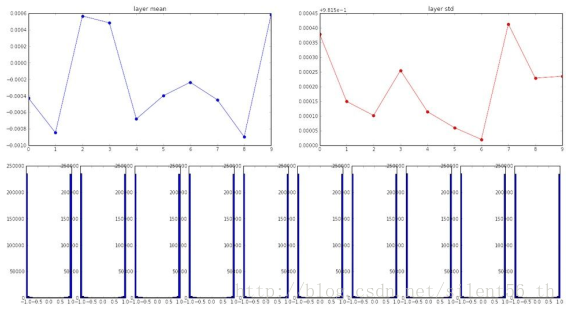
可以看出,所有的输出都是分散,被tanh约束之后基本都是1与-1,即staturated,所以gradient依旧不会传播。
所以大或者小都不合理,需要一个恰当的标准差来初始化参数,即引入下面两种初始化方式。
Xavier initialization
使用均值为0,标准差为sqrt(扇入)的高斯函数初始化所有参数。注意此方法的数学推导是基于线性激活函数的 假设,这部分是可以在tanh的原点附近的区域被满足。适用此种初始化方法,在上诉同样的网络中得到的各层神经元的分布如下图:
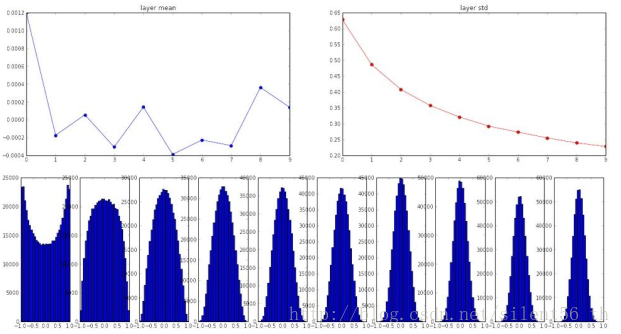
改进的Xavier
如上诉,Xavier需要线性函数的假设,这在使用ReLU为激活函数的时候不被满足。将上诉结构中的激活函数改用ReLU而后,使用Xavier的 初始化得到的各层神经元的分布如下图:
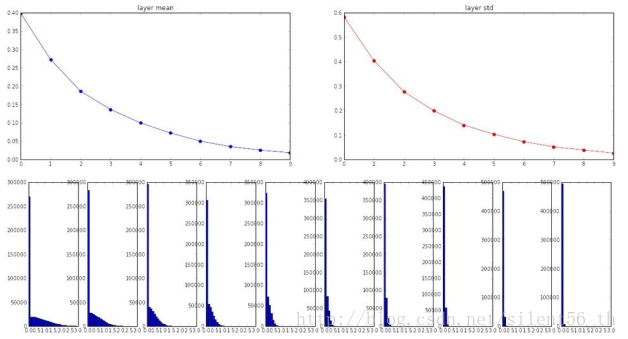
高层神经元基本为0,所以gradient几乎不传播。 为了修补这个缺点,[He et al., 2015]给出了改进的Xavier方法:用均值为0,标准差为sqrt(扇入/2)的高斯分布用于初始化参数。 使用这种方法得到的分布如下图:
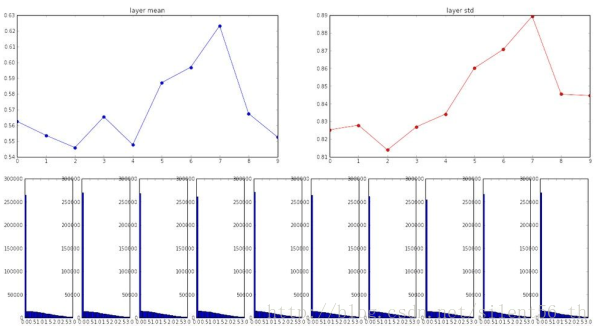
最后我们得出的结论是初始化参数仍然没有定论,尴尬!!!这个具体初始化我们要根据实验的实际和个人训练网络的经验决定。
下方是一些关于初始化参数的论文:

谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










