LSGAN(最小二乘GAN)介绍
LSGAN(最小二乘GAN)是各类GAN模型中我认为比较好的一种,实验和理论都不错,本文将带着大家一起看看LSGAN的原理。
仔细搜索和阅读论文后会发现LSGAN有两篇而且这两篇的差距还有点大,大家一定不要搞混,本文要介绍的是最小二乘GAN (least square GAN),还有一篇也叫LSGAN但是那是由齐国君教授创作的,翻译为损失敏感GAN(loss sensitive GAN). 两者有很大的差别。目前比较火热的是损失敏感GAN,这篇文章是可以和GAN,WGAN相提并论级别的了,文章是由中国的齐国君创作,他现在就任美国中佛罗 里达大学计算机系助理教授,他也是在知乎上大力推荐和解释自己的文章。我们今天说的是第一个, 最小二乘GAN,损失敏感GAN我们下次再说。
Least Squares GAN这篇文章针对的是原始GAN生成的图片质量不高以及训练过程不稳定这两个缺陷进行改进。改进方法就是将GAN的目标函数由交叉熵损失 换成最小二乘损失,而且这一个改变同时解决了两个缺陷。在解决GAN生成图片质量不高的问题时,作者解释为以交叉熵作为损失,会使得生成器不会再优化 那些被判别器识别为真实图片的生成图片,即使这些生成图片距离判别器的决策边界仍然很远,也就是距真实数据比较远,这就导致了生成器的生成图片质量 并不高。
而要使得最小二乘损失比较小,在骗过判别器的前提下还得让生成器把距离决策边界比较远的生成图片拉向决策边界,这样将在一定程度上提高生成图片与真 实图片的相似度,从而提高图片质量,由下图可以看出。
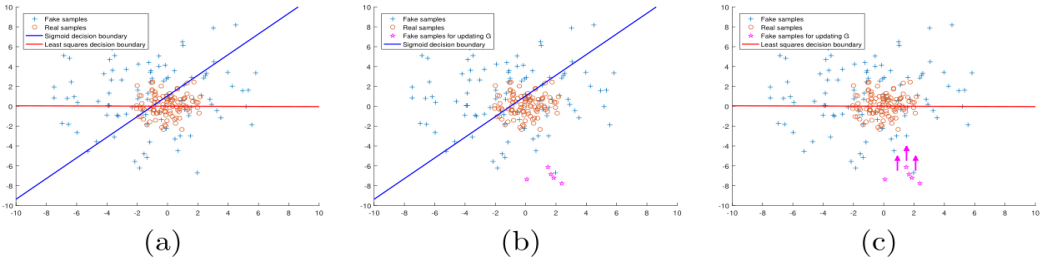
最小二乘损失可以使得GAN的训练更稳定是由于LSGAN的损失函数的设计。在之前报告中提及原始GAN存在生成器梯度消失的情况,原因是当判别器最优时生 成器的目标函数中JS散度会趋于常数log2,致使值趋于0出现梯度消失得情况。LSGAN采用最小二乘损失函数由公式1展示,给生成样本和真实样本分别编码 为a,b,G的目标函数将编码a换成编码c,这个编码表示D将G生成的样本当成真实样本,取a=-1, b=1, c=0或者a=-1, b=c=1.这样处理后将避免生成器损 失函数为0的发生。
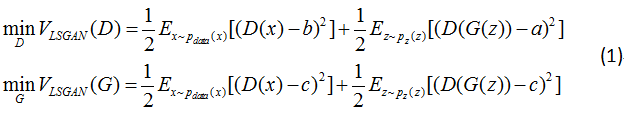
对此目标函数求判别器的最优解(可参考GAN公式推导博客)我也会 在附录中给出具体的推导过程,可以得到:
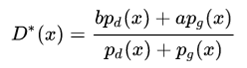
由最优解带入目标函数后,可以得到最后的生成器的解:

当选择恰当的a,b,c后,可以凑出皮尔森卡方散度,这个值是不可能为0所以便不会有梯度消失的情况发生。在结构上LSGAN与传统GAN的设计上是一样的唯 独改进的是损失函数。所以损失函数对于GAN模型还是很重要的。
小结:Least Squares GAN在利用最小二乘损失函数的设计同样解决了生成器梯度消失问题,同时在图片的生成质量上有所提高。下面是附录部分,大家可 根据个人实际选择阅读。
附录


谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










