WGAN介绍 | TwistedW's Home

WGAN可谓是继原作GAN之后又一经典之作，本文将介绍一下WGAN

WGAN的前作中对原始GAN存在的问题作了严谨的数学分析。原始GAN问题的根源可以归结为两点，一是等价优化的距离衡量（KL散度、JS散度）不合理，二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠（上升到高维时）从而导致在判别器优化的很好的时候生成器会有梯度消失的情况发生。对于生成分布与真实分布的重叠问题在WGAN前作中粗略的提及到改进的办法，那就是对生成样本和真实样本加噪声。

原文对此处描述为：通过对生成样本和真实样本加噪声，使得原本的两个低维流形“弥散”到整个高维空间，强行让它们产生不可忽略的重叠。而一旦存在重叠，JS散度就能真正发挥作用，此时如果两个分布越靠近，它们“弥散”出来的部分重叠得越多，JS散度也会越小而不会一直是一个常数，于是生成器梯度消失的问题就解决了。在训练过程中，我们可以对所加的噪声进行退火（annealing），慢慢减小其方差，到后面两个低维流形“本体”都已经有重叠时，就算把噪声完全拿掉，JS散度也能照样发挥作用，继续产生有意义的梯度把两个低维流形拉近，直到它们接近完全重合。

这样的加噪声对训练模型真的有大幅度提高吗？显然这样做是不够的，文章中解释为加噪声后JS散度的具体数值受到噪声的方差影响，随着噪声的退火，前后的数值就没法比较了，所以它不能成为Pg和Pr距离的本质性衡量。在WGAN前作设置的巨大引子的前提下，WGAN 便在随后问世了，文章从本质上解决了对生成分布和真实分布衡量问题。

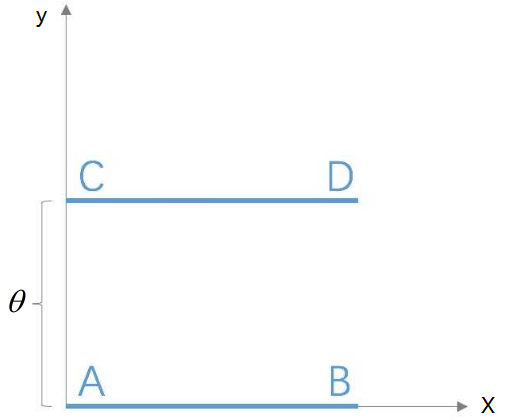
图1.二维下两均匀分布图

图1为二维空间中的两个分布和，P1在线段AB上均匀分布，P2在线段CD上均匀分布，通过控制参数可以控制着两个分布的距离远近。在此条件下分别利用KL 散度，JS散度，Wasserstein距离衡量两个分布之间的距离，结果如下，具体推证见附录。

KL散度和JS散度是突变的，要么最大要么最小，Wasserstein距离却是平滑的，要用梯度下降法优化这个参数时，前两者根本提供不了梯度，Wasserstein 距离却可以。类似地，在高维空间中如果两个分布不重叠或者重叠部分可忽略，则KL和JS既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度，这就是Wasserstein距离衡量两个分布之间距离的优势所在。

由此思想，作者通过一系列数学演算后得到和的Wasserstein距离公式。

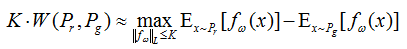
具体的推证我也有在附录中简单提及这里不做展开了，函数的Lipschitz常数为，把f用一个带参数的神经网络来表示。对于这个限制，这里其实不关心具体的K是多少，只要它不是正无穷就行，因为它只是会使得梯度变大K，并不会影响梯度的方向。作者采取了一个很工程的思想，就是限制神经网络的所有参数 (这里指权重w)不超过某个范围[-c,c]，比如w在[-0.01,0.01],此时关于输入样本x的导数也不会超过某个范围，所以一定存在某个不知道的常数K使得局部变动幅度不会超过K，Lipschitz连续条件得以满足。具体在算法实现中，只需要每次更新完w后把它clip回这个范围就可以了。此时只需要增大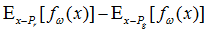就会近似真实分布与生成分布之间的Wasserstein距离（忽略常数倍数K）。需要注意的是原始GAN的判别器做的是真假二分类任务，所以最后一层是sigmoid，但是现在WGAN中的判别器做的是近似拟合Wasserstein距离，属于回归任务，所以要把最后一层的 sigmoid拿掉。