传统GAN的公式推导
GAN的整体思想在上一篇已经介绍,本篇将详细解读GAN的公式推导过程
GAN是基于最大最小博弈展开的,生成器为了生成出骗过判别器的数据不断的提高生成数据的真实性的能力,判别器为了识别出生成器生成的图片的真假不断 地提高鉴别真假的能力,到最后两者达到纳什平衡。下图形象的展示了GAN的斗争思想:
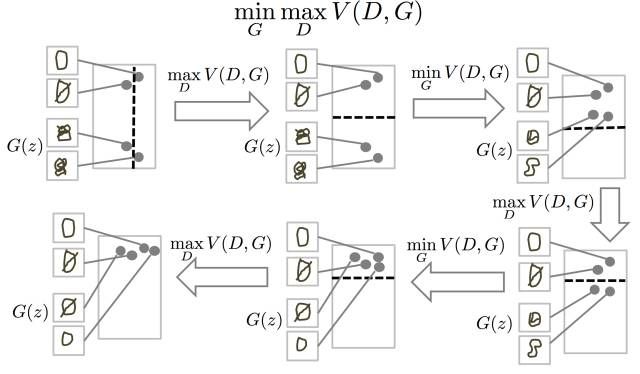
由图优化D的时候需要很好的画出黑色虚线,使它能够区分开真实数据和生成数据。优化G的时候,生成数据更加接近原始数据的样子,使得D难以区分数据 真假。如此反复直到最后再也画不出区分的黑色虚线。
GAN的应用场景
(1)GAN可以用来产生data。
(2)GAN 整个的过程就是,G产生一个自创的假数据和真数据放在一起让D来区分,在这种不停的较量中G就模拟出来了跟真实数据十分相近的数据。所以GAN 主要的应用场景就是能够学习出这样模拟分布的数据,并且可以用模拟分布代替原始数据的地方!
为什么说G学习到的是真实数据的分布呢?接下来我们从GAN的目标函数分析就可以知道。
GAN的目标函数:
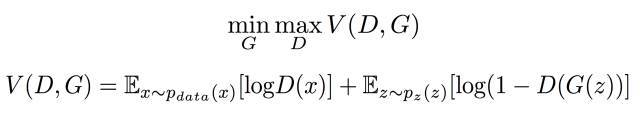
从数学上分析这个函数 首先固定G训练D :
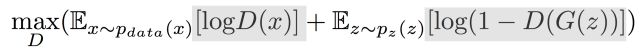
1)训练D的目的是希望这个式子的值越大越好。真实数据希望被D分成1,生成数据希望被分成0。
第一项,如果有一个真实数据被分错,那么log(D(x))«0,期望会变成负无穷大。
第二项,如果被分错成1的话,第二项也会是负无穷大。
很多被分错的话,就会出现很多负无穷,那样可以优化的空间还有很多。可以修正参数,使V的数值增大。
2)训练G ,它是希望V的值越小越好,让D分不开真假数据。
因为目标函数的第一项不包含G,是常数,所以可以直接忽略 不受影响。
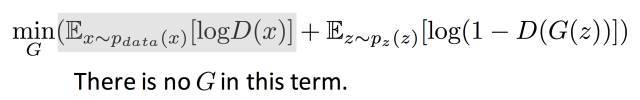
对于G来说 它希望D在划分他的时候能够越大越好,他希望被D划分1(真实数据)。

第二个式子和第一个式子等价。在训练的时候,第二个式子训练效果比较好 常用第二个式子的形式。
证明V是可以收敛导最佳解的。
(1)global optimum 存在
(2)global optimum训练过程收敛
全局优化首先固定G优化D,D的最佳情况为:
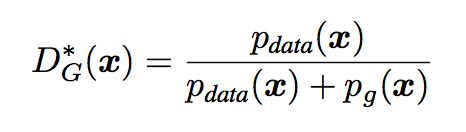
1、证明D*G(x)是最优解
由于V是连续的所以可以写成积分的形式来表示期望:
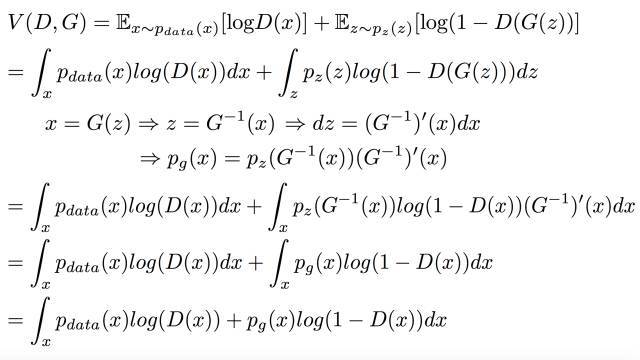
通过假设x=G(z)可逆进行了变量替换,整理式子后得到:
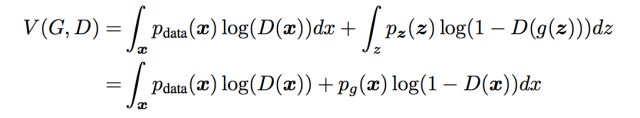
然后对V(G,D)进行最大化:对D进行优化令V取最大
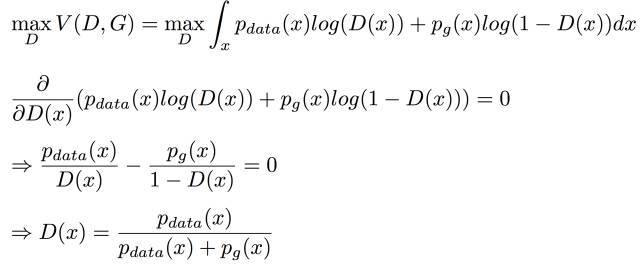
2、假设我们已经知道D*G(x)是最佳解了,这种情况下G想要得到最佳解的情况是:G产生出来的分布要和真实分布一致,即:
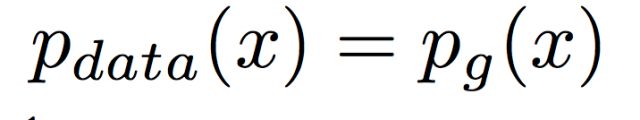
在这个条件下,$D*G(x)=\frac{1}{2}$。
接下来看G的最优解是什么,因为D的这时已经找到最优解了,所以只需要调整G ,令
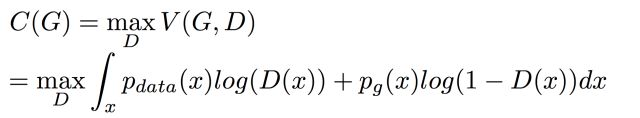
对于D的最优解我们已经知道了,D*G(x),可以直接把它带进来 并去掉前面的Max
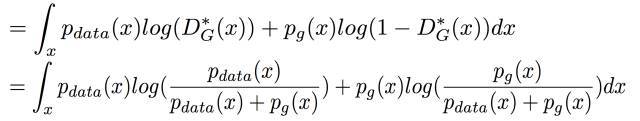
然后对 log里面的式子分子分母都同除以2,分母不动,两个分子在log里面除以2 相当于在log外面 -log(4) 可以直接提出来:
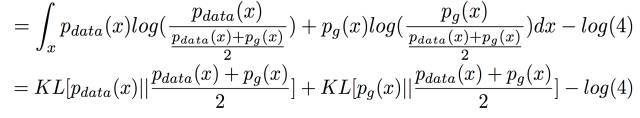
结果可以整理成两个KL散度-log(4)
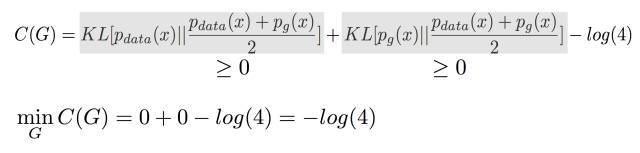
KL散度是大于等于零的,所以C的最小值是 -log(4)
当且仅当
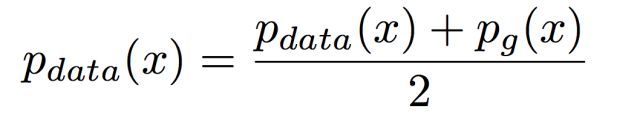
即
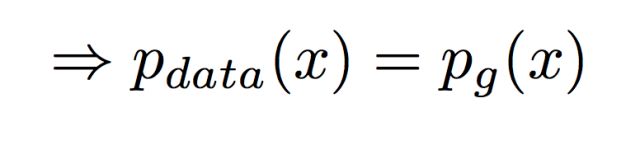
所以证明了 当G产生的数据和真实数据是一样的时候,C取得最小值也就是最佳解。 由上述推导我们可以得到最后生成器和判别器到达最优的时候,生成器学习到的生成分布其实是趋近于真实数据的分布,这样就达到了生成对抗的目的。最后 GAN可以生成出近似于真实数据的数据。但是GAN存不存在问题呢?这个答案是肯定的,要不然哪里来的这么多GAN的paper出来。本篇就不具体分析GAN问题 出在哪里,在以后的篇章里我们再具体分析。
最后分享一下我手动推导的公式笔记,大家莫嫌弃:

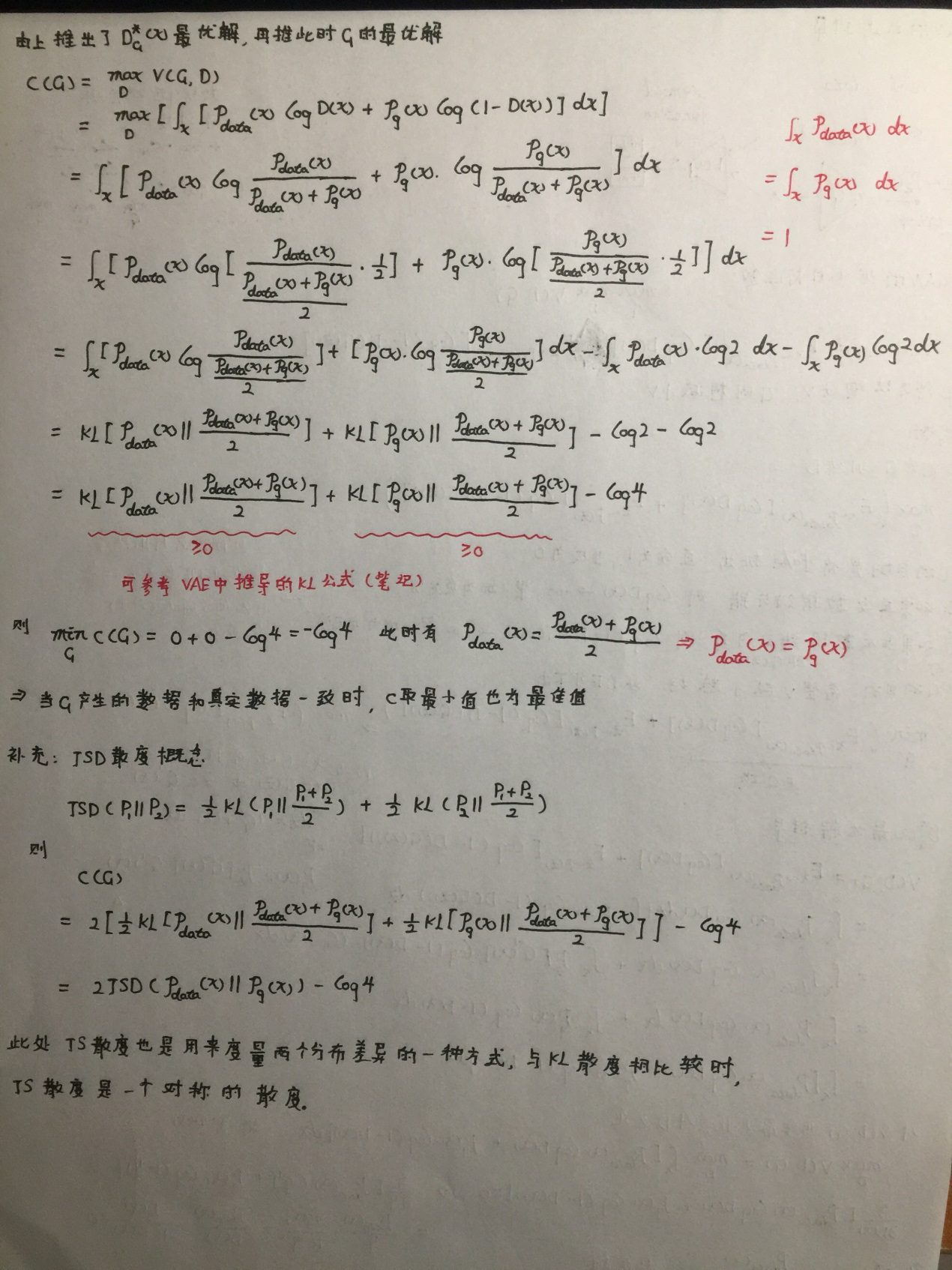
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










